题目内容
小明家订了一份报纸，寒假期间他收集了每天报纸送达时间的数据，并绘制成频率分布直方图，如图所示．（Ⅰ）根据图中的数据信息，求出众数x1和中位数x2（精确到整数分钟）；
（Ⅱ）小明的父亲上班离家的时间y在上午7：00至7：30之间，而送报人每天在x1时刻前后半小时内把报纸送达（每个时间点送达的可能性相等），求小明的父亲在上班离家前能收到报纸（称为事件A）的概率．
考点：古典概型及其概率计算公式,频率分布直方图
专题：概率与统计
分析：（Ⅰ）众数为出现频率最高的数，体现在直方图中应为最高矩形所在区间两端点的中点，中位数是从小到大排列中间位置的数，在直方图中其两边的小矩形面积相等，
（Ⅱ）考查几何概型，条件中已有父亲上班离家的时间y，再设报纸送达时间为x，关于两个变量的不等式围成平面区域内的点为所有可能，收到报纸即报纸送到时间早于父亲上班时间即想x≤y，围成平面区域为梯形，利用几何概型转化为面积之比求解即可．
（Ⅱ）考查几何概型，条件中已有父亲上班离家的时间y，再设报纸送达时间为x，关于两个变量的不等式围成平面区域内的点为所有可能，收到报纸即报纸送到时间早于父亲上班时间即想x≤y，围成平面区域为梯形，利用几何概型转化为面积之比求解即可．
解答：
解：（Ⅰ）众数最高矩形所在区间的中点，则x1=7：00
由频率分布直方图可知6：50＜x2＜7：10即410＜x2＜430
∴20×0.0033+20×0.0117+（x2-410）×0.0233
=20×0.0100+20×0.0017+（430-x2）×0.0233
解得x2=4，
（Ⅱ）设报纸送达时间为x，则小明父亲上班前能取到报纸等价于
，如图
所求概率为P=1-
=
由频率分布直方图可知6：50＜x2＜7：10即410＜x2＜430
∴20×0.0033+20×0.0117+（x2-410）×0.0233
=20×0.0100+20×0.0017+（430-x2）×0.0233
解得x2=4，
（Ⅱ）设报纸送达时间为x，则小明父亲上班前能取到报纸等价于
|
所求概率为P=1-
| ||
|
| 3 |
| 4 |
点评：本题（Ⅰ）考查在丢失原始数据的情况下利用直方图求解一些数据，尤其是众数，中位数和平均数，要理解并记忆，（Ⅱ）概率不是古典概型就是几何概型，事件可一一列举多位古典概型，否则为几何概型，设报纸送达时间为x，关于x、y的二元一次不等式组对应平面区域，转化为几何概型，求面积之比．
练习册系列答案
相关题目
在平行四边形ABCD中，
=
，
=
，
=3
，M为BC的中点，则
=（ ）
| AB |
| a |
| AD |
| b |
| AN |
| NC |
| MN |
A、-
| ||||||||
B、-
| ||||||||
C、
| ||||||||
D、-
|
下列命题中的真命题是（ ）
| A、?x∈R，x2＞0 | ||
B、?x∈R，x+
| ||
| C、?x0∈R，sinx0+cosx0=2 | ||
D、?x0∈R，ln x0＞（
|
2013年4月20日8点02分四川省雅安市芦山县（北纬30.3度，东经103.0度）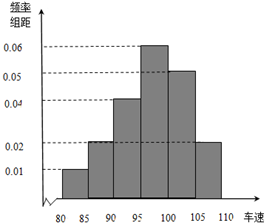
2013年国庆期间，高速公路车辆较多．某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查，将他们在某段高速公路的车速（km/h）分成六段[80，85），[85，90），[90，95），[95，100），[100，105），[105，110）后得到如下图的频率分布直方图．