题目内容
下列命题正确的个数是( )
①若
•
=0,则
=0或
=0
②(
•
)•
=
•(
•
)
③若
•
=
•
(
≠0),则
=
④若
与
不共线,
•
≥0,则
与
的夹角为锐角
⑤若
,
满足|
|>|
|且
与
同向,则
>
.
①若
| a |
| b |
| a |
| b |
②(
| a |
| b |
| c |
| a |
| b |
| c |
③若
| a |
| b |
| b |
| c |
| b |
| a |
| c |
④若
| a |
| b |
| a |
| b |
| a |
| b |
⑤若
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| A、0 | B、1 | C、2 | D、3 |
考点:命题的真假判断与应用
专题:综合题,平面向量及应用
分析:①中,
•
=0时,由数量积的定义可以得出
、
的可能情况;
②中,向量的数量积结合律不成立;
③中,向量的数量积消去率不成立;
④中,由数量积的概念得出
与
不共线时,
•
≥0,
与
夹角的可能情况;
⑤中,向量是矢量,不能比较大小.
| a |
| b |
| a |
| b |
②中,向量的数量积结合律不成立;
③中,向量的数量积消去率不成立;
④中,由数量积的概念得出
| a |
| b |
| a |
| b |
| a |
| b |
⑤中,向量是矢量,不能比较大小.
解答:
解:对于①,当
•
=0时,
=
或
=
,或
⊥
,∴①错误;
对于②,(
•
)•
=
•(
•
)不一定成立,
∵
•
与
•
都是实数,
与
也不一定共线,∴②错误;
对于③,
•
=
•
(
≠0)时,
=
不成立,
如
⊥
,
⊥
时,不一定有
=
,∴③错误;
对于④,
与
不共线时,若
•
≥0,则
与
的夹角可能为锐角或直角,∴④错误;
对于⑤,由于向量是矢量,既有大小,又有方向,∴向量不能比较大小,∴⑤错误.
综上,正确的命题个数是0.
故选:A.
| a |
| b |
| a |
| 0 |
| b |
| 0 |
| a |
| b |
对于②,(
| a |
| b |
| c |
| a |
| b |
| c |
∵
| a |
| b |
| b |
| c |
| a |
| c |
对于③,
| a |
| b |
| b |
| c |
| b |
| a |
| c |
如
| a |
| b |
| b |
| c |
| a |
| c |
对于④,
| a |
| b |
| a |
| b |
| a |
| b |
对于⑤,由于向量是矢量,既有大小,又有方向,∴向量不能比较大小,∴⑤错误.
综上,正确的命题个数是0.
故选:A.
点评:本题通过命题真假的判断,考查了平面向量的数量积的应用问题,解题时应对每一个命题进行分析,以便得出正确的结论,是基础题.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
已知f(x)=(ax+2)6,f′(x)是f(x)的导数,若f′(x)的展开式中x的系数大于f(x)的展开式中x的系数,则a的取值范围是( )
A、a>
| ||
B、0<a<
| ||
C、a>
| ||
D、a>
|
在三角形ABC中A=
,AB=1,AC=2,设点P,Q满足
=λ
,
=(1-λ)
,若
•
=-2,λ=( )
| π |
| 2 |
| AP |
| AB |
| AQ |
| AC |
| BQ |
| CP |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
如图给出的是计算
+
+
+…+
的值的一个程序框图,判断其中框内应填入的条件是( )

| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |

| A、i>10 | B、i<10 |
| C、i>20 | D、i<20 |
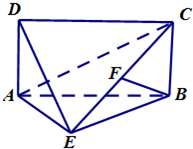 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.