题目内容
15.过双曲线的一个焦点F2作垂直干实轴的弦PQ,F1是另一焦点,若∠PF1Q=$\frac{π}{2}$,则双曲线的离心率e等于( )| A. | $\sqrt{2}$-1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$+2 | D. | $\sqrt{2}$+1 |
分析 根据题设条件求出PQ,通过∠PF2Q=90°,列出方程,推导出双曲线的离心率.
解答 解:由题意可知通径|PQ|=$\frac{2{b}^{2}}{a}$,|F1F2|=2c,|QF1|=$\frac{{b}^{2}}{a}$,
∵∠PF2Q=90°,∴b4=4a2c2,
∵c2=a2+b2,∴c4-6a2c2+a4=0,∴e4-6e2+1=0,
∴e2=3+2$\sqrt{2}$或e2=3-2$\sqrt{2}$(舍去),
∵e>1,∴e=1+$\sqrt{2}$.
故选:D.
点评 这道题数量间的关系比较繁琐,推导过程中要多一点耐心.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.若点P(x0,y0)是曲线y=xex上任意一点,则|x0-y0-4|的最小值为( )
| A. | 4 | B. | $3\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | 2 |
20.已知实数x,y满足$\left\{\begin{array}{l}{x-2y+1>0}\\{x<2}\\{x+y-1>0}\end{array}\right.$,若z=2x-2y-1,则z的取值范围为( )
| A. | (-$\frac{5}{3}$,5) | B. | (-$\frac{5}{3}$,0) | C. | [0,5] | D. | [-$\frac{5}{3}$,5] |
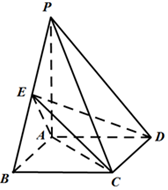 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA垂直底面ABCD,PA=AB=2,E是棱PB的中点.