题目内容
已知P是直线l:3x-4y+11=0上的动点,PA、PB是圆C:(x-1)2+(y-1)2=1的两条切线,圆心为C,那么四边形PACB面积的最小值是( )
A、
| ||
B、2
| ||
C、
| ||
D、2
|
考点:圆的切线方程
专题:直线与圆
分析:S四边形PACB=S△PAC+S△PBC,当|PC|取最小值时,|PA|=|PB|取最小值,即S△PAC=S△PBC取最小值,由此能够求出四边形PACB面积的最小值.
解答:
 解:把直线与圆相离如图,S四边形PACB=S△PAC+S△PBC
解:把直线与圆相离如图,S四边形PACB=S△PAC+S△PBC
而S△PAC=
|PA|•|CA|=
|PA|,
S△PBC=
|PB|•|CB|=
|PB|,
又|PA|=
,|PB|=
,
∴当|PC|取最小值时,|PA|=|PB|取最小值,
即S△PAC=S△PBC取最小值,此时,CP⊥l,|CP|=
=
=2,
则S△PAC=S△PBC=
×
=
,
即四边形PACB面积的最小值是
.
故选C.
 解:把直线与圆相离如图,S四边形PACB=S△PAC+S△PBC
解:把直线与圆相离如图,S四边形PACB=S△PAC+S△PBC而S△PAC=
| 1 |
| 2 |
| 1 |
| 2 |
S△PBC=
| 1 |
| 2 |
| 1 |
| 2 |
又|PA|=
| |PC|2-1 |
| |PC|2-1 |
∴当|PC|取最小值时,|PA|=|PB|取最小值,
即S△PAC=S△PBC取最小值,此时,CP⊥l,|CP|=
| |3×1-4×1+11| | ||
|
| 10 |
| 5 |
则S△PAC=S△PBC=
| 1 |
| 2 |
| 22-1 |
| ||
| 2 |
即四边形PACB面积的最小值是
| 3 |
故选C.
点评:本题考查直线和圆的位置关系,解题时要认真审题,在解答过程中要合理地运用数形结合思想.

练习册系列答案
相关题目
某算法的程序如图所示,若输入x=2,则电脑屏上显示的结果为( )


| A、16 | B、4 | C、y=0 | D、0 |
已知某几何体的三视图如图所示,则该几何体的体积等于( )


A、
| ||
| B、32 | ||
C、
| ||
D、
|
 如图,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.
如图,直棱柱ABCD-A1B1C1D1中,底面ABCD是直角梯形,∠BAD=∠ADC=90°,AB=2AD=2CD=2.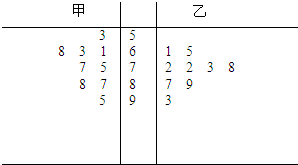 某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图
某班级甲乙两个小组各9名同学的期中考试数学成绩 (单位:分)的茎叶图如图