题目内容
6.设n≥2,且n∈N*,证明:(1+$\frac{1}{3}$)(1+$\frac{1}{5}$)(1+$\frac{1}{7}$)…(1+$\frac{1}{2n-1}$)>$\frac{\sqrt{2n+1}}{2}$.分析 直接利用数学归纳法的证明步骤证明不等式,(1)验证n=1时不等式成立;(2)假设当n=k(k≥1)时成立,利用放缩法证明n=k+1时,不等式也成立.
解答 证明:(1)当n=2时,不等式左边=1+$\frac{1}{3}$=$\frac{4}{3}$=$\frac{8}{6}$=$\frac{\sqrt{64}}{6}$,不等式右边=$\frac{\sqrt{5}}{2}$=$\frac{3\sqrt{5}}{6}$=$\frac{\sqrt{45}}{6}$,不等式成立,
(2)假设n=k时,不等式成立,即:(1+$\frac{1}{3}$)(1+$\frac{1}{5}$)(1+$\frac{1}{7}$)…(1+$\frac{1}{2k-1}$)>$\frac{\sqrt{2k+1}}{2}$,
那么当n=k+1是,即(1+$\frac{1}{3}$)(1+$\frac{1}{5}$)(1+$\frac{1}{7}$)…(1+$\frac{1}{2k-1}$)(1+$\frac{1}{2k+1}$)>$\frac{\sqrt{2k+1}}{2}$•(1+$\frac{1}{2k+1}$)=$\frac{\sqrt{2k+1}}{2}$•$\frac{2k+2}{2k+1}$=$\frac{k+1}{\sqrt{2k+1}}$,
∵(2k+1)(2k+3)<4(k+1)2,
∴$\sqrt{2k+1}$•$\sqrt{2k+3}$<2(k+1),
∴$\frac{k+1}{\sqrt{2k+1}}$>$\frac{\sqrt{2k+3}}{2}$,
∴当n=k+1时,不等式也成立,
根据(1)(2)可得不等式对所有的n≥2都成立.
点评 本题是中档题,考查数学归纳法的证明步骤,注意不等式的证明方法,放缩法的应用,考查逻辑推理能力.

| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
| A. | S10>S9 | B. | a8=0 | ||
| C. | d<0 | D. | S7与S8均为Sn的最大值 |
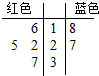 袋中有六张形状、质地等完全相同的卡片,其中红色卡片四张,蓝色卡片两张,每张卡片都标有一个数字,如茎叶图所示:
袋中有六张形状、质地等完全相同的卡片,其中红色卡片四张,蓝色卡片两张,每张卡片都标有一个数字,如茎叶图所示: