题目内容
18.已知圆O:x2+y2=1,圆M:(x-a)2+(y-a+4)2=1.若圆M上存在点P,过点P作圆O的两条切线,切点为A,B,使得∠APB=60°,则实数a的取值范围为[$2-\frac{\sqrt{2}}{2},2+\frac{\sqrt{2}}{2}$].分析 由题意画出图形,利用两点间的距离关系求出OP的距离,再由题意得到关于a的不等式求得答案.
解答 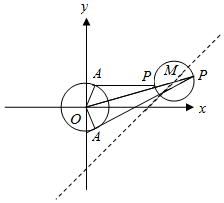 解:如图
解:如图
圆O的半径为1,圆M上存在点P,过点P作圆O的两条切线,切点为A,B,使得∠APB=60°,
则∠APO=30°,在Rt△PAO中,PO=2,
又圆M的半径等于1,圆心坐标M(a,a-4)
∴|PO|min=|MO|-1,|PO|max=|MO|+1,
∵$|MO|=\sqrt{{a}^{2}+(a-4)^{2}}$,
∴由$\sqrt{{a}^{2}+(a-4)^{2}}-1≤2≤\sqrt{{a}^{2}+(a-4)^{2}}+1$,解得:2$-\frac{\sqrt{2}}{2}≤a≤2+\frac{\sqrt{2}}{2}$.
故答案为:[$2-\frac{\sqrt{2}}{2},2+\frac{\sqrt{2}}{2}$]
点评 本题主要考查直线和圆的位置关系的应用,利用数形结合将条件进行等价转化是解决本题的关键,是中档题.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
9.已知数列{an}满足a1=10,an+1=$\frac{{a}_{n}}{{a}_{n}+2}$,则{an}中第一个小于$\frac{1}{10000}$的数是( )
| A. | a12 | B. | a13 | C. | a14 | D. | a15 | ||||
| E. | a16 |
3.不等式|3x-2|>1的解集为( )
| A. | (-∞,-$\frac{1}{3}$)∪(1,+∞) | B. | (-$\frac{1}{3}$,1) | C. | (-∞,$\frac{1}{3}$)∪(1,+∞) | D. | ($\frac{1}{3}$,1) |