题目内容
 已知△ABC是边长为3的等边三角形,点D、E分别是边AB,AC上的点,且满足
已知△ABC是边长为3的等边三角形,点D、E分别是边AB,AC上的点,且满足| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
(1)求证:A1D⊥EC;
(2)设P为线段BC上的一点,试求直线PA1与平面A1BD所成角的正切的最大值.
考点:直线与平面所成的角,平面与平面垂直的性质
专题:空间位置关系与距离
分析:(1)等边△ABC的边长为3,且
=
=
,求得AD和AE的值.进而由余弦定理得DE,根据AD2+DE2=AE2,判断AD⊥DE折叠后A1D⊥DE,根据平面A1DE⊥平面BCED,又平面利用线面垂直的判定定理推断出A1D⊥平面BCED,进而可知A1D⊥EC.
(2)作PH⊥BD于点H,连结A1H、A1P,由(1)有A1D⊥平面BCED,而PH?平面BCED,推断出A1D⊥PH,又A1D∩BD=D,进而根据线面垂直的判定定理知PH⊥平面A1BD,推断出∠PA1H是直线PA1与平面A1BD所成的角,设出PB,分别表示出BH,PH,DH进利用勾股定理求得A1H的表达式,继而在Rt△PA1H中,表示出tan∠PA1H,对x进行分类讨论,利用函数的思想求得tan∠PA1H的最大值.
| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
(2)作PH⊥BD于点H,连结A1H、A1P,由(1)有A1D⊥平面BCED,而PH?平面BCED,推断出A1D⊥PH,又A1D∩BD=D,进而根据线面垂直的判定定理知PH⊥平面A1BD,推断出∠PA1H是直线PA1与平面A1BD所成的角,设出PB,分别表示出BH,PH,DH进利用勾股定理求得A1H的表达式,继而在Rt△PA1H中,表示出tan∠PA1H,对x进行分类讨论,利用函数的思想求得tan∠PA1H的最大值.
解答:
证明:(1)因为等边△ABC的边长为3,且
=
=
,
所以AD=1,AE=2.在△ADE中,∠DAE=60°,
由余弦定理得DE=
=
.
因为AD2+DE2=AE2,
所以AD⊥DE.
折叠后有A1D⊥DE,
因为平面A1DE⊥平面BCED,又平面A1DE∩平面BCED=DE,
A1D?平面A1DE,A1D⊥DE,所以A1D⊥平面BCED
故A1D⊥EC.
(2)如图,作PH⊥BD于点H,连结A1H、A1P,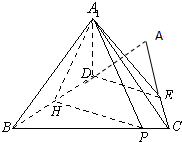
由(1)有A1D⊥平面BCED,而PH?平面BCED,
所以A1D⊥PH,又A1D∩BD=D,所以PH⊥平面A1BD,
所以∠PA1H是直线PA1与平面A1BD所成的角,
设PB=x(0≤x≤3),则BH=
,PH=
,DH=BD-BH=2-
所以A1H=
=
所以在Rt△PA1H中,tan∠PA1H=
=
①若x=0,则tan∠PA1H=
=
=0,
②若x≠0则tan∠PA1H=
=
=
令
=t(t≥
),y=20t2-8t+1
因为函数y=20t2-8t+1在t≥
上单调递增,所以ymin=20×
-
+1=
所以tan∠PA1H的最大值为
=
(此时点P与C重合)
| AD |
| DB |
| CE |
| EA |
| 1 |
| 2 |
所以AD=1,AE=2.在△ADE中,∠DAE=60°,
由余弦定理得DE=
| 12+22-2×1×2×cos60° |
| 3 |
因为AD2+DE2=AE2,
所以AD⊥DE.
折叠后有A1D⊥DE,
因为平面A1DE⊥平面BCED,又平面A1DE∩平面BCED=DE,
A1D?平面A1DE,A1D⊥DE,所以A1D⊥平面BCED
故A1D⊥EC.
(2)如图,作PH⊥BD于点H,连结A1H、A1P,

由(1)有A1D⊥平面BCED,而PH?平面BCED,
所以A1D⊥PH,又A1D∩BD=D,所以PH⊥平面A1BD,
所以∠PA1H是直线PA1与平面A1BD所成的角,
设PB=x(0≤x≤3),则BH=
| x |
| 2 |
| ||
| 2 |
| x |
| 2 |
所以A1H=
| DH2+A1D2 |
|
所以在Rt△PA1H中,tan∠PA1H=
| PH |
| A1H |
| ||
|
①若x=0,则tan∠PA1H=
| PH |
| A1H |
| ||
|
②若x≠0则tan∠PA1H=
| PH |
| A1H |
| ||
|
| ||||||
|
令
| 1 |
| x |
| 1 |
| 3 |
因为函数y=20t2-8t+1在t≥
| 1 |
| 3 |
| 1 |
| 9 |
| 8 |
| 3 |
| 5 |
| 9 |
所以tan∠PA1H的最大值为
| ||||
|
3
| ||
| 5 |
点评:本题主要考查了线面垂直的判定定理和性质,二面角的求法.解题的关键是找到或作出所求二面角.

练习册系列答案
相关题目
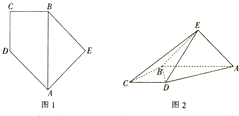 已知直角梯形ABCD的下底与等腰直角三角形ABE的斜边重合,AB⊥BC,且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连接EC、ED,得到四棱锥E-ABCD(如图2).
已知直角梯形ABCD的下底与等腰直角三角形ABE的斜边重合,AB⊥BC,且AB=2CD=2BC(如图1),将此图形沿AB折叠成直二面角,连接EC、ED,得到四棱锥E-ABCD(如图2). 如图,一个底面半径为
如图,一个底面半径为