题目内容
已知函数f(x)=
,方程f2(x)+mf(x)=0有五个不同的实数解时,m的取值范围为 .
|
考点:根的存在性及根的个数判断
专题:函数的性质及应用
分析:由方程可得f(x)=0或f(x)=-m,作出f(x)的图象,利用数形结合即可得到结论.
解答:
 解:由f2(x)+mf(x)=0得f(x)[f(x)+m]=0,
解:由f2(x)+mf(x)=0得f(x)[f(x)+m]=0,
即f(x)=0或f(x)=-m,
作出f(x)的图象如图:
由图象可知f(x)=0的根有两个x=0或x=3,
要使方程f2(x)+mf(x)=0有五个不同的实数解时,
则方程f(x)=-m有三个根,
此时满足0<-m<1,
解得-1<m<0,
故答案为:-1<m<0
 解:由f2(x)+mf(x)=0得f(x)[f(x)+m]=0,
解:由f2(x)+mf(x)=0得f(x)[f(x)+m]=0,即f(x)=0或f(x)=-m,
作出f(x)的图象如图:
由图象可知f(x)=0的根有两个x=0或x=3,
要使方程f2(x)+mf(x)=0有五个不同的实数解时,
则方程f(x)=-m有三个根,
此时满足0<-m<1,
解得-1<m<0,
故答案为:-1<m<0
点评:本题主要考查方程根的个数的应用,利用数形结合是解决本题的关键.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
已知向量
=(2,1),
=(3,2),若
⊥(
+λ
),则实数λ等于( )
| a |
| b |
| a |
| a |
| b |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
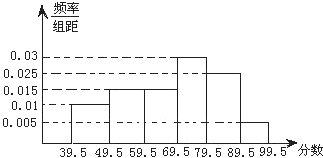 如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图:观察图形,回答下列问题:
如图,从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)整理后画出的频率分布直方图如图:观察图形,回答下列问题: