题目内容
五个人站成一排照相，其中甲与乙不相邻，且甲与丙也不相邻的不同站法有 ．
考点：排列、组合及简单计数问题
专题：应用题,排列组合
分析：分为两种情况：甲在两头，甲不在两头，即可得出结论．
解答：
解：分为两种情况：甲在两头，则排列方法为2×2×（3×2×1）=24种；
甲不在两头，则排列方法为3×2×（2×1）=12种，
故共24+12=36种排法．
故答案为：36．
甲不在两头，则排列方法为3×2×（2×1）=12种，
故共24+12=36种排法．
故答案为：36．
点评：解决此类问题的关键是特殊元素优先考虑，不同的问题利用不同的方法解决如相邻问题用捆绑，不相邻问题用插空等方法．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
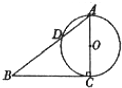如图，已知Rt△ABC的两条直角边AC，BC的长分别为3cm，4cm，以AC为直径的圆与AB交于点D，求 BD的长．
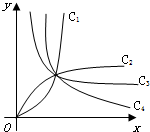如图的曲线是幂函数y=xn在第一象限内的图象，已知n分别取a，b，c，d四个值，与曲线C1，C2，C3，C4相应，则a，b，c，d四个值从小到大依次为
根据下面的要求，求满足1+2+3+…+n＞500的最小的自然数n．已知
=（1，2），
=（-3，x），若
∥
，则x=（ ）
| a |
| b |
| a |
| b |
| A、1.5 | B、-1.5 |
| C、-6 | D、6 |