题目内容
13.试用-个角的正弦(或余弦)形式表示下列各式:(1)sinα-cosα;
(2)$\sqrt{3}$sinα+cosα;
(3)$\frac{1}{2}$cos15°+$\frac{\sqrt{3}}{2}$sin15°;
(4)3sinα+4cosα.
分析 使用两角和差的正弦公式化简即可.
解答 解:(1)sinα-cosα=$\sqrt{2}$($\frac{\sqrt{2}}{2}$sinα-$\frac{\sqrt{2}}{2}$cosα)=$\sqrt{2}$sin(α-$\frac{π}{4}$);
(2)$\sqrt{3}$sinα+cosα=2($\frac{\sqrt{3}}{2}$sinα+$\frac{1}{2}$cosα)=2sin(α+$\frac{π}{6}$);
(3)$\frac{1}{2}$cos15°+$\frac{\sqrt{3}}{2}$sin15°=sin30°cos15°+cos30°sin15°=sin45°;
(4)3sinα+4cosα=5($\frac{3}{5}$sinα+$\frac{4}{5}$cosα)=5sin(α+φ)(其中sinφ=$\frac{4}{5}$,cosφ=$\frac{3}{5}$).
点评 本题考查了两角和差的正弦公式,属于基础题.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
3.抛物线的顶点在原点,焦点在x轴上,其通径的两端与顶点连成的三角形的面积为4.则此抛物线的方程是( )
| A. | y2=8$\sqrt{2}$x | B. | y2=±4$\sqrt{2}$x | C. | y2=±4x | D. | y2=±8$\sqrt{2}$x |
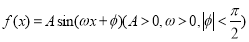 的部分图象如图所示.
的部分图象如图所示.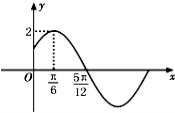
 ,
,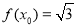 ,若g(x)=1+2cos2x,求g(x0)的值;
,若g(x)=1+2cos2x,求g(x0)的值; 上有解,求实数a的取值范围.
上有解,求实数a的取值范围. 的最小正周期是( )
的最小正周期是( ) B.
B. C.
C. D.
D.
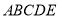 中,四边形
中,四边形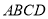 是正方形,正三角形
是正方形,正三角形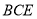 的边长为2,
的边长为2,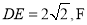 为线段
为线段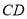 上一点,
上一点,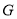 为线段
为线段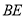 的中点.
的中点.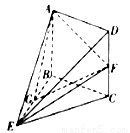
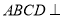 平面
平面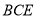 ;
;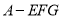 的体积.
的体积.