题目内容
17.三棱锥P-ABC中,PA=AB=BC=2,PB=AC=2$\sqrt{2}$,PC=2$\sqrt{3}$,则三棱锥P-ABC的外接球的表面积为12π.分析 可得△PAC是Rt△.PBC是Rt△.可得三棱锥P-ABC的外接球的球心、半径,即可求出三棱锥P-ABC的外接球的表面积.
解答 解:∵AP=2,AC=2$\sqrt{2}$,PC=2$\sqrt{3}$,∴AP2+AC2=PC2
∴△PAC是Rt△.
∵PB=2$\sqrt{2}$,BC=2,PC=2$\sqrt{3}$,∴∴△PBC是Rt△.
∴取PC中点O,则有OP=OC=OA=OB=$\sqrt{3}$,
∴O为三棱锥P-ABC的外接球的球心,半径为$\sqrt{3}$.
∴三棱锥P-ABC的外接球的表面积为4πR2=12π.
故答案为:12π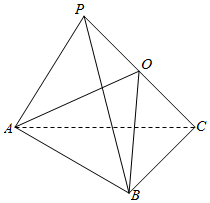
点评 本题考查了三棱锥P-ABC的外接球的表面积,考查学生的计算能力,确定三棱锥P-ABC的外接球的球心、半径是关键.属于中档题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
19.$\frac{1-{i}^{3}}{1-i}$=( )
| A. | -i | B. | i | C. | 1+i | D. | 1 |
9.已知直线ax+y+1=0与x+(a+$\frac{3}{2}$)y+2=0平行,则实数a=( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$或-2 | D. | 2或-$\frac{1}{2}$ |
6.将-$\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα化成Asin(α+β)(A>0,0<β<2π)的形式,以下式子正确的是( )
| A. | sin(α+$\frac{4π}{3}$) | B. | sin(α+$\frac{7π}{6}$) | C. | -sin(α+$\frac{π}{3}$) | D. | sin(α-$\frac{2π}{3}$) |
7.命题“?x∈[1,2],x2-2x-a≤0”为真命题的一个充分不必要条件是( )
| A. | a≥0 | B. | a≤0 | C. | a≥1 | D. | a≤1 |