题目内容
2.求和:(1)$\sum_{k=1}^{10}$(3+2k);
(2)(2+$\frac{1}{3}$)+(4+$\frac{1}{9}$)+(6+$\frac{1}{27}$)+…+(2n+$\frac{1}{{3}^{n}}$);
(3)(a-1)+(a2-1)+(a3-1)+…+(an-1)
分析 分别根据等比数列和等差数列的前n项和公式计算即可.
解答 解:(1)$\sum_{k=1}^{10}$(3+2k)=3+21+3+22+…+3+210=3×10+$\frac{2(1-{2}^{10})}{1-2}$=30+(211-2)=2076,
(2)(2+$\frac{1}{3}$)+(4+$\frac{1}{9}$)+(6+$\frac{1}{27}$)+…+(2n+$\frac{1}{{3}^{n}}$)=(2+4+6+…+2n)+($\frac{1}{3}$+$\frac{1}{{3}^{2}}$+$\frac{1}{{3}^{3}}$+…+$\frac{1}{{3}^{n}}$)=$\frac{n(2+2n)}{2}$+$\frac{\frac{1}{3}(1-{3}^{-n})}{1-\frac{1}{3}}$n2+n+$\frac{1}{2}$-$\frac{1}{2•{3}^{n}}$,
(3(a-1)+(a2-1)+(a3-1)+…+(an-1)=(a+a2+a3+…+an)-n,
当a=1时,(a-1)+(a2-1)+(a3-1)+…+(an-1)=0,
当a≠1时,(a-1)+(a2-2)+(a3-3)+…+(an-n)=$\frac{a(1-{a}^{n})}{1-a}$-n
点评 本题考查了等差数列和等比数列当前n项和公式,培养了学生的运算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.若$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是夹角为$\frac{π}{3}$的两个单位向量,则$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$;$\overrightarrow{b}$=-3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
17.cos(-1920°)的值为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
7.已知函数f(x)=2sin2(ωx+$\frac{π}{6}$)(ω>0)在区间[$\frac{π}{6}$,$\frac{2π}{3}$]内单调递增,则ω的最大值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
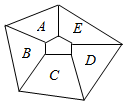 如图,在A,B,C,D,E五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为( )
如图,在A,B,C,D,E五个区域中栽种3种植物,要求同一区域中只种1种植物,相邻两区域所种植物不同,则不同的栽种方法的总数为( )