题目内容
已知奇函数f(x)在(-∞,0)上单调递增,且f(2)=0,则不等式(x-1)•f(x-1)>0的解集是( )
| A、(-1,3) |
| B、(-∞-1) |
| C、(-∞-1)∪(3,+∞) |
| D、(-1,1)∪(1,3) |
考点:奇偶性与单调性的综合
专题:计算题,函数的性质及应用
分析:先根据函数f(x)的奇偶性以及函数在区间(-∞,0)上的单调性,判断函数在区间(0,+∞)的单调性,再把不等式(x-1)f(x-1)>0变形为两个不等式组,根据函数的单调性分情况解两个不等式组,所得解集求并集即可.
解答:
解:∵函数f(x)为奇函数且在(-∞,0)上单调递增,
∴f(x)在(0,+∞)上也单调递增,
∴(x-1)f(x-1)>0可变形为
①或
②
又∵函数f(x)为奇函数且f(2)=0,∴f(-2)=-f(2)=0
∴不等式组①的解为
即x>3;
不等式组②的解为
,即x<-1.
∴不等式(x-1)f(x-1)>0的解集为(-∞,-1)∪(3,+∞).
故选:C.
∴f(x)在(0,+∞)上也单调递增,
∴(x-1)f(x-1)>0可变形为
|
|
又∵函数f(x)为奇函数且f(2)=0,∴f(-2)=-f(2)=0
∴不等式组①的解为
|
不等式组②的解为
|
∴不等式(x-1)f(x-1)>0的解集为(-∞,-1)∪(3,+∞).
故选:C.
点评:本题主要考查综合运用函数的单调性与奇偶性解不等式,研究此类题最好作出函数图象辅助判断.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
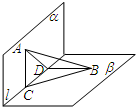 已知平面α⊥平面β,α∩β=l,A∈α,B∈β,AC⊥l,垂足为C,BD⊥l,垂足为D(点C,D不重合),若AC>BD,则( )
已知平面α⊥平面β,α∩β=l,A∈α,B∈β,AC⊥l,垂足为C,BD⊥l,垂足为D(点C,D不重合),若AC>BD,则( )| A、AD>BC,∠ABC>∠BAD |
| B、AD>BC,∠ABC<∠BAD |
| C、AD<BC,∠ABC>∠BAD |
| D、AD<BC,∠ABC<∠BAD |
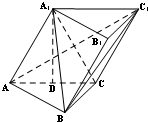 如图所示,已知三棱柱ABC-A1B1C1,点A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,BA1⊥AC1.
如图所示,已知三棱柱ABC-A1B1C1,点A1在底面ABC上的射影恰为AC的中点D,∠BCA=90°,AC=BC=2,BA1⊥AC1.