��Ŀ����
11����ֱ������ϵxOy�У�ֱ��l�IJ���������$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$��t�Dz�������������ԭ��Ϊ���㣬x���������Ϊ���ᣬ����������ϵ������C�ļ����귽��Ϊ��=4cos�ȣ�����д��ֱ��l����ͨ���̺�����C��ֱ�����귽�̣�
�������P��ֱ������Ϊ��1��1����ֱ��l������C�Ľ���ΪA��B����|PA|•|PB|��ֵ��
���� ������ֱ�ߵIJ������̼��������ͨ���̣�����C�ļ����귽���������C��ֱ�����귽�̣�
�������A��B�����꣬����Բ�ķ��̣����ɸ���Τ�ﶨ���������t1t2=-2����|PA|•|PB|=حt1t2ح��
��� �⣺����ֱ��l����ͨ����Ϊx-y=0���ɦ�=4cos�ȣ����2=4��cos�ȣ���x2+y2-4x=0��
������C��ֱ�����귽��x2+y2-4x=0��
�����ɵ�A��B����ֱ��l�ϣ��������Ƕ�Ӧ�IJ����ֱ�Ϊt1��t2��
���A��B������ΪA��1+$\frac{\sqrt{2}}{2}$t1��1+$\frac{\sqrt{2}}{2}$t1����B��1+$\frac{\sqrt{2}}{2}$t2��1+$\frac{\sqrt{2}}{2}$t2����
��ֱ��l�IJ������̴���Բ����Ϊx2+y2-4x=0��
������t2-2=0����
��t1��t2�ֱ��Ƿ��̢ٵĽ⣬�Ӷ�t1t2=-2��
��|PA|•|PB|=حt1t2ح=2��
|PA|•|PB|��ֵ2��
���� ���⿼���˲������̻�Ϊ��ͨ���̡������귽�̵�Ӧ�ã�������������������������������е��⣮

��ϰ��ϵ�д�
 ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ͬ����ϰ���ϴ�ѧ������ϵ�д�
ͬ����ϰ���ϴ�ѧ������ϵ�д� ����ϰ�⽭��ϵ�д�
����ϰ�⽭��ϵ�д�
�����Ŀ
2�����š�ȫ��������������У����н�ӭ�������߷壮�����´���ʼ��Ȫ�Ǹ�ҽԺ���ƾ��Ѿ���һƬæµ�����ȶȲ������������Ž��е���ͳ���ڼ䷢�ָ�ҽԺ���������У����ٶ��ǡ������������е�һҽԺ������40���ﱦ������������10���ǡ�������������
��������ҽԺ��ǰ���������б����а��ֲ����������ȡ7��������������ѯ��
�����е�һҽԺ������һ�������г�ȡ���ٸ���
������7�������г�ȡ��������������죬������������ǡ������ͬҽԺ�Ҿ������������ĸ��ʣ�
��II�������������ݣ��ܷ���85%�İ�����Ϊһ������������ij�����ҽԺ�йأ�
K2=$\frac{{n��ad-bc{��^2}}}{��a+b����c+d����a+c����b+d��}$��
��������ҽԺ��ǰ���������б����а��ֲ����������ȡ7��������������ѯ��
�����е�һҽԺ������һ�������г�ȡ���ٸ���
������7�������г�ȡ��������������죬������������ǡ������ͬҽԺ�Ҿ������������ĸ��ʣ�
��II�������������ݣ��ܷ���85%�İ�����Ϊһ������������ij�����ҽԺ�йأ�
| P��k��k���� | 0.40 | 0.25 | 0.15 | 0.10 |
| k�� | 0.708 | 1.323 | 2.072 | 2.706 |
6������˵����ȷ���ǣ�������
| A�� | С��90��Ľ������ | |
| B�� | �۽DZ��ǵڶ����ǣ��ڶ����DZ��Ƕ۽� | |
| C�� | �������ĽǴ��ڵڶ����Ľ� | |
| D�� | �Ǧ���Ǧµ��ձ���ͬ���Ǧ���Ǧ¿��ܲ���� |
16����ͼ���ڡ�ABC�У�$\overrightarrow{AN}=\frac{1}{4}\overrightarrow{NC}$��P��BN�ϵ�һ�㣬��$\overrightarrow{AP}=m\overrightarrow{AB}+\frac{2}{11}\overrightarrow{AC}$����ʵ��m��ֵΪ��������
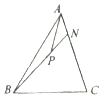

| A�� | $\frac{9}{11}$ | B�� | $\frac{2}{11}$ | C�� | $\frac{3}{11}$ | D�� | $\frac{1}{11}$ |
3��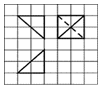 ��ͼ��ʾ������ֽ��С�����εı߳�Ϊ1������������ij�������������ͼ����������ı����Ϊ��������
��ͼ��ʾ������ֽ��С�����εı߳�Ϊ1������������ij�������������ͼ����������ı����Ϊ��������
 ��ͼ��ʾ������ֽ��С�����εı߳�Ϊ1������������ij�������������ͼ����������ı����Ϊ��������
��ͼ��ʾ������ֽ��С�����εı߳�Ϊ1������������ij�������������ͼ����������ı����Ϊ��������| A�� | 2��1+2$\sqrt{2}$+$\sqrt{3}$�� | B�� | 2��1+$\sqrt{2}$+$\sqrt{3}$�� | C�� | $4{+}2\sqrt{6}$ | D�� | 4��1+$\sqrt{2}$�� |
20����֪һ������3��4��5��s��t��ƽ������4����λ����m����������ʵ��s��t����3��4��5��s��t��m������������ȡһ����ȡ������4�ĸ��ʵ����ֵΪ��������
| A�� | $\frac{1}{6}$ | B�� | $\frac{1}{3}$ | C�� | $\frac{1}{2}$ | D�� | $\frac{2}{3}$ |
1��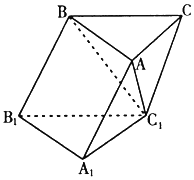 ��ͼ����б��������ABC-A1B1C1�У���BAC=90�㣬BC1��AC����PΪAC1�ϵ�һ�����㣬���P�ڵ���ABC�ϵ���ӰH���ڣ�������
��ͼ����б��������ABC-A1B1C1�У���BAC=90�㣬BC1��AC����PΪAC1�ϵ�һ�����㣬���P�ڵ���ABC�ϵ���ӰH���ڣ�������
 ��ͼ����б��������ABC-A1B1C1�У���BAC=90�㣬BC1��AC����PΪAC1�ϵ�һ�����㣬���P�ڵ���ABC�ϵ���ӰH���ڣ�������
��ͼ����б��������ABC-A1B1C1�У���BAC=90�㣬BC1��AC����PΪAC1�ϵ�һ�����㣬���P�ڵ���ABC�ϵ���ӰH���ڣ�������| A�� | ֱ��AB�� | B�� | ֱ��BC�� | C�� | ֱ��AC�� | D�� | ��ABC�ڲ� |
