题目内容

1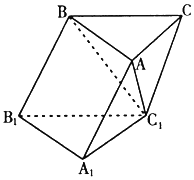．如图，在斜三棱柱中ABC-A1B1C1中，∠BAC=90°，BC1⊥AC，点P为AC1上的一个动点，则点P在底面ABC上的射影H必在（　　）
A．直线AB上B．直线BC上C．直线AC上D．△ABC内部

分析 要知C1在底面ABC上的射影H的位置，需要看过这个点向底面做射影，观察射影的位置，根据AC与一个平面上的两条直线垂直，得到AC与两条直线组成的面垂直，根据面面垂直的判断和性质，即可得出结果．

解答 解：∵∠BAC=90°，∴AC⊥AB；
又AC⊥BC1，且AB∩BC1=B，
∴AC⊥平面ABC1；
又AC?平面ABC，
∴平面ABC1⊥平面ABC，
∴C1在平面ABC上的射影H必在两平面的交线AB上．
故选：A．

点评 本题考查了棱柱的结构特征以及直线与平面垂直的判定、平面与平面垂直的判定和性质的应用问题．

练习册系列答案
相关题目
11．在直角坐标系xOy中，直线l的参数方程是$\left\{\begin{array}{l}{x=1+\frac{\sqrt{2}}{2}t}\\{y=1+\frac{\sqrt{2}}{2}t}\end{array}\right.$（t是参数），以坐标原点为极点，x轴的正半轴为极轴，建立极坐标系，曲线C的极坐标方程为ρ=4cosθ．
（Ⅰ）写出直线l的普通方程和曲线C的直角坐标方程；
（Ⅱ）设点P的直角坐标为（1，1），直线l与曲线C的交点为A，B，求|PA|•|PB|的值．
12．已知f（x）是定义在R上的奇函数，且当x∈（-∞，0）时，不等式f（x）+xf′（x）＜0成立，若a=πf（π），b=（-2）f（-2），c=f（1），则a，b，c的大小关系是（　　）
A．a＞b＞cB．c＞b＞aC．c＞a＞bD．a＞c＞b
9．集合A={x|-1＜x＜1}，B={x|x＜a}．
（1）若A∩B=∅，求a的取值范围；
（2）若A∪B={x|x＜1}，求a的取值范围．
16．执行如图的程序框图，若输入的x的值为29，则输出的n的值为（　　）
A．1B．2C．3D．4
6．公园263年左右，我国数学家刘徽发现当圆内接正多边形的边数无限增加时，多边形面积可无限逼近圆的面积，并创立了“割圆术”．利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14，这就是著名的“徽率”．如图是利用刘徽的“割圆术”思想设计的一个程序框图，则输出n的值为24．
参考数据：$\sqrt{3}$=1.732，sin15°≈0.2588，sin7.5°≈0.1305．
13．已知点P是平行四边形ABCD所在平面外一点，如果$\overrightarrow{AB}$=（2，-1，-4），$\overrightarrow{AD}$=（4，2，0），$\overrightarrow{AP}$=（-1，2，-1）
（1）求证：$\overrightarrow{AP}$是平面ABCD的法向量
（2）求平行四边形ABCD的面积．
10．如图所示算法，若输入的x的值为2017，则算法执行后的输出结果是（　　）
A．2016B．2017C．2D．0
4．用秦九韶算法计算多项式f（x）=3x5+2x3-8x+5在x=2时的值时，V4的值为48．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网