题目内容
5.等比数列{an}中,若a4a5=1,a8a9=16,则公比q等于( )| A. | $\sqrt{2}$ | B. | 2 | C. | -2 | D. | $±\sqrt{2}$ |
分析 由等比数列的性质得${q}^{4}=\frac{{a}_{8}{a}_{9}}{{a}_{4}{a}_{5}}$=$\frac{16}{1}=16$.a4a5=${{a}_{1}}^{2}{q}^{7}$=1>0,由此能求出公比q的值.
解答 解:∵等比数列{an}中,a4a5=1,a8a9=16,
∴${q}^{4}=\frac{{a}_{8}{a}_{9}}{{a}_{4}{a}_{5}}$=$\frac{16}{1}=16$.
又a4a5=${a}_{1}{q}^{3}•{a}_{1}{q}^{4}={{a}_{1}}^{2}{q}^{7}$=1>0,
∴q>0,
解得公比q=$\sqrt{2}$.
故选:A.
点评 本题考查等比数列的公比的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
相关题目
15.某几何体的三视图如图,其正视图中的曲线部分为半圆,则该几何体的表面积为( )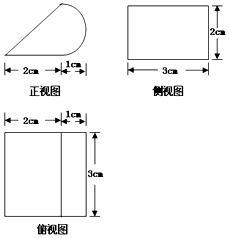

| A. | (19+π)cm2 | B. | (22+4π)cm2 | C. | (10+6$\sqrt{2}$+4π)cm2 | D. | (13+6$\sqrt{2}$+4π)cm2 |
17.在△ABC中,“cosB=$\frac{1}{2}$”是“A、B、C成等差数列”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分又非必要条件 |