题目内容
椭圆
+y2=1上的点到直线x-y+6=0的最小距离是( )
| x2 |
| 3 |
A、
| ||
B、2
| ||
C、3
| ||
D、4
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:椭圆
+y2=1上的点(
cosα,sinα),0≤θ<2π,求得点到直线的距离d=
=
,可得当cos(α+
)=-1时,取得最小值,从而求得结论.
| x2 |
| 3 |
| 3 |
|
| ||
|
|2cos(α+
| ||
|
| π |
| 6 |
解答:
解:设椭圆
+y2=1上的点(
cosα,sinα),0≤θ<2π,则
点到直线的距离d=
=
,
∴cos(α+
)=-1时,距离最小为2
.
故选:B.
| x2 |
| 3 |
| 3 |
点到直线的距离d=
|
| ||
|
|2cos(α+
| ||
|
∴cos(α+
| π |
| 6 |
| 2 |
故选:B.
点评:本题考查点到直线的距离公式,余弦函数的定义域和值域,比较基础.

练习册系列答案
相关题目
四面体ABCD中,已知AB=CD=
,AC=BD=
,AD=BC=
,则四面体ABCD的外接球的表面积为( )
| 29 |
| 34 |
| 37 |
| A、25π | B、45π |
| C、50π | D、100π |
设函数f(x)在R 上有定义,给出下列函数:
(1)y=-|f(x)|;
(2)y=f(|x|);
(3)y=-f(-x);
(4)y=f(x)-f(-x);
其中为奇函数的有( )
(1)y=-|f(x)|;
(2)y=f(|x|);
(3)y=-f(-x);
(4)y=f(x)-f(-x);
其中为奇函数的有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
已知扇形的周长为8cm,圆心角为2弧度,则该扇形的面积为( )
| A、8 | ||
B、
| ||
| C、4 | ||
| D、2 |
已知角α的终边经过点P(3t,-4t)(t≠0),则sinα+cosα的值为( )
A、
| ||
B、
| ||
C、-
| ||
D、±
|
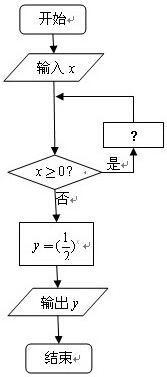 执行如图程序,若输入x=10,要求输出y=4,则在图中“?”处可填入的算法语句是( )
执行如图程序,若输入x=10,要求输出y=4,则在图中“?”处可填入的算法语句是( )①x=x-1②x=x-2③x=x-3④x=x-4.
| A、①②③ | B、②③ |
| C、②③④ | D、③④ |
已知椭圆的中心在原点,长轴长为6,一条准线方程为x=9,则该椭圆的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设f(x)=
,若f(0)是f(x)的最小值,则a的取值范围为( )
|
| A、[-1,2] |
| B、[-1,0] |
| C、[1,2] |
| D、[0,2] |