题目内容
下列说法不正确的是( )
| A、对于函数y=f(x),若f(a)=0,则a是函数y=f(x)的零点 |
| B、方程f(x)=0有实数根,则函数y=f(x)有零点 |
| C、如果函数y=f(x)在区间[a,b]上图象是连续不断的一条曲线,且f(a)•f(b)<0,那么函数y=f(x)在区间[a,b]内至少有一个零点 |
| D、如果函数y=f(x)在区间[a,b]上图象是连续不断的一条曲线,且f(a)•f(b)>0,那么函数y=f(x)在区间[a,b]内一定有一个零点 |
考点:函数零点的判定定理
专题:函数的性质及应用
分析:据函数零点的定义,函数零点的判定定理,A、B、C都正确,通过举反例可得D不正确,从而得出结论.
解答:
解:根据函数零点的定义,函数零点的判定定理,A、B、C都正确,
而D不正确,如f(x)=x 在区间[2,4]上满足f(2)f(4)>0,
但函数y=f(x)在区间[2,4]内没有零点,
故选:D.
而D不正确,如f(x)=x 在区间[2,4]上满足f(2)f(4)>0,
但函数y=f(x)在区间[2,4]内没有零点,
故选:D.
点评:本题主要考查函数零点的定义,函数零点的判定定理,利用特殊值代入法,排除不符合条件的选项,是一种简单有效的方法,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将一枚骰子抛掷两次,若先后出现的点数分别为x、y,则满足x=2y的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
已知(1+x+x2+x3)(x+
)n的展开式中没有常数项,则n的一个可能值为( )
| 1 |
| x4 |
| A、11 | B、12 | C、13 | D、14 |
已知x,y∈R+,且xy2=8,则4x+y的最小值为( )
A、4
| ||
B、6
| ||
| C、6 | ||
| D、2 |
等比数列{an}中,a4+a5=3,a3a6=2,则a2=( )
| A、8 | ||
B、
| ||
C、8或
| ||
D、
|
计算sin46°cos16°+sin44°cos106°的结果等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设集合A={x|y=
},集合B={y|y=x2,x∈R},则A∪B=( )
| x+1 |
| A、ϕ |
| B、[0,+∞) |
| C、[1,+∞) |
| D、[-1,+∞) |

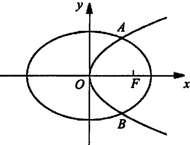 如图,已知椭圆C1:
如图,已知椭圆C1: