题目内容
已知正项数列{an}中,a1=1,a2=2,2an2=an+12+an-12,则a6等( )
| A、16 | ||
| B、4 | ||
C、2
| ||
| D、45 |
考点:数列递推式
专题:等差数列与等比数列
分析:由2an2=an+12+an-12,(n≥2),得{an2}是等差数列,首项a12=1,公差为a22-a12=4-1=3,由此能求出
.
| a | 6 |
解答:
解:∵2an2=an+12+an-12,(n≥2),
∴{an2}是等差数列,首项a12=1,公差为a22-a12=4-1=3,
∴an2=1+3(n-1)=3n-2,
∴a62=3×6-2=16,
∴
=4.
故选:B.
∴{an2}是等差数列,首项a12=1,公差为a22-a12=4-1=3,
∴an2=1+3(n-1)=3n-2,
∴a62=3×6-2=16,
∴
| a | 6 |
故选:B.
点评:本题考查数列的第6项的求法,是中档题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
已知O是△ABC所在平面内一点,且|
|2+|
|2=|
|2+|
|2=|
|2+|
|2,则O是△ABC的( )
| OC |
| AB |
| OB |
. |
| AC |
| OA |
| BC |
| A、内心 | B、垂心 | C、外心 | D、重心 |
已知m>0,n>0,向量
=(1,1),向量
=(m,n-3),且
⊥(
+
),则
+
的最小值为( )
| a |
| b |
| a |
| a |
| b |
| 1 |
| m |
| 4 |
| n |
| A、9 | B、16 | C、18 | D、8 |
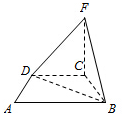 一几何体如图所示,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°.FC⊥平面ABCD,CB=CD=CEF=1.
一几何体如图所示,四边形ABCD是等腰梯形,AB∥CD,∠DAB=60°.FC⊥平面ABCD,CB=CD=CEF=1.