题目内容
已知函数f(x)=
,若函数g(x)=f(x)+k有三个零点,则k的取值范围是 .
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:利用数形结合的思想,若函数g(x)=f(x)+k有三个零点,也就是f(x)=g(x)-k,即y=-k与f(x)有三个交点,只要求出f(x)的最小值即可.
解答:
解:如图所示,∵f(x)=
(x≥0)
∴f′(x)=
令f′(x)=0,
则x=1,
当0≤x<1时,f′(x)>0,函数f(x)为单调递增函数,
当x>1时,f′(x)<0,函数f(x)为单调递减函数,
∴当x=1时,函数f(x)有最大值,最大值为f(1)=
,
∴-k=
即k=-
,
∴k的取值范围是(-
,0)

| x |
| ex |
∴f′(x)=
| 1-x |
| ex |
令f′(x)=0,
则x=1,
当0≤x<1时,f′(x)>0,函数f(x)为单调递增函数,
当x>1时,f′(x)<0,函数f(x)为单调递减函数,
∴当x=1时,函数f(x)有最大值,最大值为f(1)=
| 1 |
| e |
∴-k=
| 1 |
| e |
即k=-
| 1 |
| e |
∴k的取值范围是(-
| 1 |
| e |

点评:本题考查了函数零点的问题,利用数形结合的思想,转化为求函数的最值问题,属于中档题.

练习册系列答案
相关题目
已知α∈(0,
),a=(sinα)cosα,b=(sinα)sinα,c=(cosα)sinα,则a、b、c的大小关系是( )
| π |
| 4 |
| A、a>b>c |
| B、c>a>b |
| C、b>a>c |
| D、c>b>a |
在△ABC中,a=2011,b=1,则sinA:sinB等于( )
| A、1:1 | B、1:2011 |
| C、2011:1 | D、不确定 |
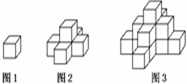 如图1是一个水平摆放的小正方体木块,图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是
如图1是一个水平摆放的小正方体木块,图2、图3是由这样的小正方体木块叠放而成,按照这样的规律继续逐个叠放下去,那么在第七个叠放的图形中小正方体木块数应是