题目内容
已知函数f(x)=
+2lnx-1,a∈R.
(Ⅰ)当a=1时,求函数f(x)的单调区间;
(Ⅱ)求函数f(x)在区间(0,e]上的最小值.
| a |
| x |
(Ⅰ)当a=1时,求函数f(x)的单调区间;
(Ⅱ)求函数f(x)在区间(0,e]上的最小值.
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:导数的概念及应用
分析:(Ⅰ)a=1时,f′(x)=
,从而确定f(x)在(0,
)递减,在(
,+∞)递增,
(Ⅱ)分别讨论①a≤0时,②0<a<2e时,③a≥2e时的情况,从而求出最小值.
| 2x-1 |
| x2 |
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)分别讨论①a≤0时,②0<a<2e时,③a≥2e时的情况,从而求出最小值.
解答:
解:∵f′(x)=
,
(Ⅰ)a=1时,f′(x)=
,
令f′(x)>0,解得:x>
,
令f′x)<0,解得:0<x<
,
∴f(x)在(0,
)递减,在(
,+∞)递增,
(Ⅱ)①a≤0时,f′(x)>0,f(x)在(0,+∞)递增,
∴f(x)在(0,e)无最小值,
②0<a<2e时,
由(Ⅰ)得:
f(x)min=f(
)=1+2ln
,
③a≥2e时,
由(Ⅰ)得:
f(x)min=f(e)=
+1.
| 2x-a |
| x2 |
(Ⅰ)a=1时,f′(x)=
| 2x-1 |
| x2 |
令f′(x)>0,解得:x>
| 1 |
| 2 |
令f′x)<0,解得:0<x<
| 1 |
| 2 |
∴f(x)在(0,
| 1 |
| 2 |
| 1 |
| 2 |
(Ⅱ)①a≤0时,f′(x)>0,f(x)在(0,+∞)递增,
∴f(x)在(0,e)无最小值,
②0<a<2e时,
由(Ⅰ)得:
f(x)min=f(
| a |
| 2 |
| a |
| 2 |
③a≥2e时,
由(Ⅰ)得:
f(x)min=f(e)=
| a |
| e |
点评:本题考察了函数的单调性,函数的最值问题,导数的应用,是一道综合题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
y=cosx•sinx是( )
| A、奇函数 |
| B、偶函数 |
| C、既是奇函数也是偶函数 |
| D、既不是奇函数也不是偶函数 |
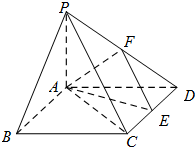 如图在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=
如图在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=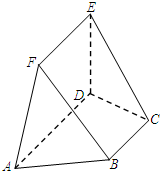 如图,在五面体ABCDEF中,已知DE⊥平面ABCD,AD∥BC,∠BAD=60°AB=2,DE=EF=1.
如图,在五面体ABCDEF中,已知DE⊥平面ABCD,AD∥BC,∠BAD=60°AB=2,DE=EF=1. 如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点.
如图,已知正方体ABCD-A1B1C1D1的棱长为2,M为正方形AA1D1D的中心,N为棱AB的中点.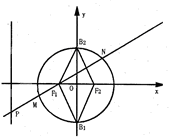 如图,椭圆C:
如图,椭圆C: