题目内容
已知三条直线a、b、c，若这三条直线两两相交，且交点分别为A、B、C，试判断这三条直线是否共面．
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：利用设a，b确定一个平面α，由已知条件利用公理二能推导出c?α，从而这三条直线a，b，c共面于α．
解答：
解：如图，三条直线a、b、c两两相交，
且交点分别为A、B、C，
设a，b确定一个平面α，
∵B∈a，C∈a，A∈b，C∈b，
∴A∈α，B∈α，
又∵A∈c，B∈c，
∴c?α，
∴三条直线a，b，c共面于α．
∴这三条直线共面．
且交点分别为A、B、C，
设a，b确定一个平面α，
∵B∈a，C∈a，A∈b，C∈b，
∴A∈α，B∈α，
又∵A∈c，B∈c，
∴c?α，
∴三条直线a，b，c共面于α．
∴这三条直线共面．
点评：本题考查三条直线是否共面的判断，是基础题，解题时要认真审题，注意公理二的灵活运用．
练习册系列答案
相关题目
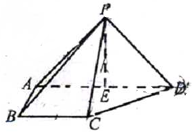如图，在四棱锥P-ABCD中，侧面PAD⊥底面ABCD，侧棱PA=PD=
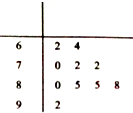为了保护生态和环境，某市不再完全以GDP考核辖区内各县政府的政绩，广大群众的幸福指数成为考核县政府政绩的又一个重要指标，从而成立了市政府幸福办公室，其主要工作是随机抽查群众的幸福指数，为市政府提供最基础的原始数据．该办公室某工作人员在一次随机抽查了10名A县群众后，绘制了如图的茎叶图．