题目内容
14.某农业生态园有果树60000棵,其中樱桃树有4000棵.为调查果树的生长情况,采用分层抽样的方法抽取一个容量为300的样本,则样本中樱桃树的数量为20棵.分析 先求出每个个体被抽到的概率,用该层的个体数乘以每个个体被抽到的概率,就等于该层应抽取的个体数.
解答 解:每个个体被抽到的概率等于$\frac{300}{60000}$=$\frac{1}{200}$,
设样本中抽取樱桃树的数量为x,则$\frac{x}{4000}$=$\frac{1}{200}$
解得x=20.
故答案为:20.
点评 本题考查了分层抽样的定义和方法,用每层的个体数乘以每个个体被抽到的概率等于该层应抽取的个体数,是基础题.

练习册系列答案
相关题目
4.过抛物线y2=4x的焦点F作斜率为1的直线,交抛物线于A、B两点,若$\overrightarrow{AF}$=λ$\overrightarrow{FB}$(λ>1),则λ等于( )
| A. | $\sqrt{2}$+1 | B. | $\sqrt{3}$+1 | C. | $\sqrt{5}$+1 | D. | 2$\sqrt{2}$+3 |
5.已知随机变量ξ的分布列为
且E(ξ)=2,D(ξ)=$\frac{1}{2}$,则P(-1<ξ<2)=( )
| ξ | 1 | 2 | 3 |
| P | p1 | p2 | p3 |
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
9.函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则f($\frac{2π}{3}$)=( )
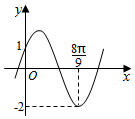

| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
19.“a<1”是“函数f(x)=|x-a|+|x-1|在区间[1,+∞)上为增函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |