题目内容
6．已知圆C：（x-2）2+（y-3）2=1，（0，3）且斜率为k的直线l与圆C有两个不同的交点M，N，且$\overrightarrow{OM}$•$\overrightarrow{ON}$=$\frac{84}{5}$，则实数k的值为$\frac{1}{2}$．分析 联立方程组消元，设M（x1，y1），N（x2，y2），根据根与系数的关系得出x1x2，y1y2，代入数量积公式列方程解出k．
解答 解：直线l的方程为y=kx+3，
联立方程组$\left\{\begin{array}{l}{（x-2）^{2}+（y-3）^{2}=1}\\{y=kx+3}\end{array}\right.$，消元得：（k2+1）x2-4x+3=0，
设M（x1，y1），N（x2，y2），则x1x2=$\frac{3}{{k}^{2}+1}$，x1+x2=$\frac{4}{{k}^{2}+1}$．
∴y1y2=（kx1+3）（kx2+3）=k2x1x2+3k（x1+x2）+9=$\frac{3{k}^{2}}{{k}^{2}+1}$+$\frac{12k}{{k}^{2}+1}$+9．
∴$\overrightarrow{OM}$•$\overrightarrow{ON}$=x1x2+y1y2=$\frac{3}{{k}^{2}+1}$+$\frac{3{k}^{2}}{{k}^{2}+1}$+$\frac{12k}{{k}^{2}+1}$+9=$\frac{84}{5}$，
解得，k=$\frac{1}{2}$．
故答案为：$\frac{1}{2}$．
点评 本题考查了平面向量的数量积运算，根与系数的关系，属于中档题．
练习册系列答案
相关题目
16．已知函数f（x）=log2（ax+4）在（1，2]上单调递减，则实数a的值可以是（ ）
| A． | 1 | B． | -1 | C． | -2 | D． | -3 |
17．
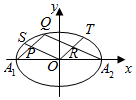如图，A1，A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A1，A2的三点，直线QA1，QA2，OS围成一个平行四边形OPQR，则|OS|2+|OT|2=（ ）
如图，A1，A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A1，A2的三点，直线QA1，QA2，OS围成一个平行四边形OPQR，则|OS|2+|OT|2=（ ）| A． | 5 | B． | 3+$\sqrt{5}$ | C． | 9 | D． | 14 |
11．已知函数f（x）=2cos（ωx+θ）（0＜θ＜π，ω＞0）为奇函数，其图象与直线y=2相邻两交点的距离为π，则函数f（x）（ ）
| A． | 在[${\frac{π}{6}$，$\frac{π}{3}}$]上单调递减 | B． | 在[${\frac{π}{6}$，$\frac{π}{3}}$]上单调递增 | ||
| C． | 在[-$\frac{π}{6}$，$\frac{π}{4}}$]上单调递减 | D． | 在[-$\frac{π}{6}$，$\frac{π}{4}}$]上单调递增 |