题目内容
9.函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的图象如图所示,则f($\frac{2π}{3}$)=( )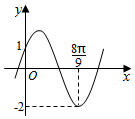
| A. | $\sqrt{3}$ | B. | 1 | C. | -1 | D. | -$\sqrt{3}$ |
分析 由函数f(x)的图象经过点(0,1),可解得sinφ=$\frac{1}{2}$,结合范围|φ|<$\frac{π}{2}$,可求φ,又函数f(x)的图象经过点($\frac{8π}{9}$,-2),由五点作图法解得ω,可得函数解析式,进而利用诱导公式,特殊角的三角函数值即可计算得解.
解答 解:∵函数f(x)=2sin(ωx+φ)的图象经过点(0,1),
∴1=2sinφ,解得sinφ=$\frac{1}{2}$,
∵|φ|<$\frac{π}{2}$,
∴φ=$\frac{π}{6}$,故f(x)=2sin(ωx+$\frac{π}{6}$),
又∵函数f(x)=2sin(ωx+φ)的图象经过点($\frac{8π}{9}$,-2),
∴-2=2sin($\frac{8π}{9}$ω+$\frac{π}{6}$),由五点作图法解得:$\frac{8π}{9}$ω+$\frac{π}{6}$=$\frac{3π}{2}$,解得:ω=$\frac{3}{2}$,
∴f(x)=2sin($\frac{3}{2}$x+$\frac{π}{6}$),
∴f($\frac{2π}{3}$)=2sin($\frac{3}{2}$×$\frac{2π}{3}$+$\frac{π}{6}$)=-1.
故选:C.
点评 本题考查由函数的部分图象确定函数的解析式,本题解题的关键是确定初相的值,这里利用代入点的坐标求出初相,属于基础题.

练习册系列答案
相关题目
17.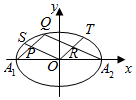 如图,A1,A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
如图,A1,A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
 如图,A1,A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS围成一个平行四边形OPQR,则|OS|2+|OT|2=( )
如图,A1,A2为椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1的长轴的左、右端点,O为坐标原点,S,Q,T为椭圆上不同于A1,A2的三点,直线QA1,QA2,OS围成一个平行四边形OPQR,则|OS|2+|OT|2=( )| A. | 5 | B. | 3+$\sqrt{5}$ | C. | 9 | D. | 14 |
19. 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象向右平移$\frac{π}{6}$个单位得到g(x)的部分图象如图所示,则y=Acos(ωx+φ)的单调递增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象向右平移$\frac{π}{6}$个单位得到g(x)的部分图象如图所示,则y=Acos(ωx+φ)的单调递增区间为( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象向右平移$\frac{π}{6}$个单位得到g(x)的部分图象如图所示,则y=Acos(ωx+φ)的单调递增区间为( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象向右平移$\frac{π}{6}$个单位得到g(x)的部分图象如图所示,则y=Acos(ωx+φ)的单调递增区间为( )| A. | [kπ-$\frac{5}{6}$π,kπ-$\frac{π}{3}$],k∈Z | B. | [kπ-$\frac{1}{3}$π,kπ+$\frac{π}{6}$],k∈Z | ||
| C. | [kπ-$\frac{7}{12}$π,kπ-$\frac{π}{12}$],k∈Z | D. | [kπ-$\frac{1}{12}$π,kπ+$\frac{5π}{12}$],k∈Z |