题目内容
过点M（3，1），作圆（x-2）2+（y-3）2=1的两条切线，切点为A、B
（1）求两切线MA、MB的方程；
（2）求线段AB的长度．
（1）求两切线MA、MB的方程；
（2）求线段AB的长度．
考点：圆的切线方程
专题：直线与圆
分析：（1）根据直线和圆相切，转化为圆心到直线的距离等于半径即可求直线MA、MB的方程；
（2）根据条件求出切点A的坐标，求直线AB的方程，利用弦长公式进行求解即可．
（2）根据条件求出切点A的坐标，求直线AB的方程，利用弦长公式进行求解即可．
解答：
解：（1）由圆的标准方程得圆心坐标为C（2，3），半径R=1，
若切线斜率k不存在，则直线方程为x=3，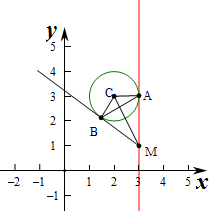
此时圆心到直线的距离d=3-2=1，满足直线和圆相切．
当切线斜率k存在时，设过M点的圆的切线方程为y+1=k（x-3）．即kx-y-3k-1=0．∵圆心C（2，3）到直线的距离为1．
即
=
=1，
∴k=-
．
∴所求的切线方程为y+1=-
（x-3）或x=3，
即15x+8y-37=0或x=3．
（2）由图象可知A（3，3），
CM的斜率k=
=-2，
则弦AB的斜率k=
，
则AB的方程为y-3=
（x-3），
即x-2y+3=0，
圆心C（2，3）到直线x-2y+3=0的距离d=
=
，
则线段AB的长度为2
=2
=2
=
．
若切线斜率k不存在，则直线方程为x=3，
此时圆心到直线的距离d=3-2=1，满足直线和圆相切．
当切线斜率k存在时，设过M点的圆的切线方程为y+1=k（x-3）．即kx-y-3k-1=0．∵圆心C（2，3）到直线的距离为1．
即
| |2k-3-3k-1| | ||
|
| |k+4| | ||
|
∴k=-
| 15 |
| 8 |
∴所求的切线方程为y+1=-
| 15 |
| 8 |
即15x+8y-37=0或x=3．
（2）由图象可知A（3，3），
CM的斜率k=
| 3-1 |
| 2-3 |
则弦AB的斜率k=
| 1 |
| 2 |
则AB的方程为y-3=
| 1 |
| 2 |
即x-2y+3=0，
圆心C（2，3）到直线x-2y+3=0的距离d=
| |2-6+3| | ||
|
| 1 | ||
|
则线段AB的长度为2
| R2-d2 |
1-
|
|
4
| ||
| 5 |
点评：本题主要考查直线和圆的位置关系的应用，利用直线和圆相切的等价条件是解决本题的关键．
练习册系列答案
相关题目
已知
，
为不共共线的非零向量，且|
|=|
|=1，则以下四个向量中模最大者为（ ）
| e1 |
| e2 |
| e1 |
| e2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知点A（x，1，2）和点B（2，3，4），且|AB|=2
，则实数x的值是（ ）
| 6 |
| A、-3或4 | B、3或-4 |
| C、6或-2 | D、6或2 |