题目内容
(1)计算:
-(
)0+(
)-0.5+
;
(2)计算
.
| 1 | ||
|
| 3 |
| 5 |
| 9 |
| 4 |
| 4 | (
| ||
(2)计算
lg5•lg8000+(lg2
| ||||
lg600-
|
考点:对数的运算性质
专题:函数的性质及应用
分析:(1)利用根式与分数指数幂的运算法则求解.
(2)利用对数的性质和运算法则求解.
(2)利用对数的性质和运算法则求解.
解答:
解:(1)
-(
)0+(
)-0.5+
=
+1-1+
+e-
=e+
.
(2)lg5•lg8000+(lg2
)2=lg5(3+3lg2)+3(lg2)2
=3lg5+3lg2(lg5+lg2)=3,
lg600-
lg0.036-
lg0.1
=(lg6+2)-lg
=lg6+2-lg
=4,
∴
=
.
| 1 | ||
|
| 3 |
| 5 |
| 9 |
| 4 |
| 4 | (
| ||
=
| 2 |
| 2 |
| 3 |
| 2 |
=e+
| 2 |
| 3 |
(2)lg5•lg8000+(lg2
| 3 |
=3lg5+3lg2(lg5+lg2)=3,
lg600-
| 1 |
| 2 |
| 1 |
| 2 |
=(lg6+2)-lg
|
=lg6+2-lg
| 6 |
| 100 |
∴
lg5•lg8000+(lg2
| ||||
lg600-
|
| 3 |
| 4 |
点评:本题考查根式与分数指数幂的化简运算,考查对数的性质和运算法则的应用,是基础题.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
x2<1是-1<x<1的什么条件( )
| A、充分必要条件 |
| B、必要不充分条件 |
| C、充分不必要条件 |
| D、既不充分与不必要 |
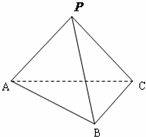 如图,在三棱锥P-ABC中,PA=PB=PC=AC=4,AB=BC=2
如图,在三棱锥P-ABC中,PA=PB=PC=AC=4,AB=BC=2