题目内容
如图，在等腰三角形ABC中，底边BC=2，| AD |
| DC |
| AE |
| EB |
| BD |
| AC |
| 1 |
| 2 |
| CE |
| AB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：根据题意，结合等腰三角形ABC，建立平面直角坐标系，利用向量的坐标运算解答共线与数量积的问题，容易得出答案．
解答：
解：∵在等腰三角形ABC中，底边BC=2，
∴取BC的中点O为坐标原点，建立平面直角坐标系，如图所示；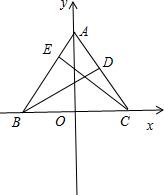
则B（-1，0），C（1，0）；
设A（0，a）（a＞0），
∵
=
，∴D（
，
）；
∴
=（
，
），
=（1，-a）；
∵
•
=-
，∴
-
=-
，
解得a=2，∴A（0，2）；
又∵2
=3
，∴
=
；
设点E（x，y），∴（x，y-2）=
（-1，-2）；
解得
，即E（-
，
）；
∴
=（-
，
），
=（-1，-2），
∴
•
=-
×（-1）+
×（-2）=0．
故答案为：0．
∴取BC的中点O为坐标原点，建立平面直角坐标系，如图所示；
则B（-1，0），C（1，0）；
设A（0，a）（a＞0），
∵
| AD |
| DC |
| 1 |
| 2 |
| a |
| 2 |
∴
| BD |
| 3 |
| 2 |
| a |
| 2 |
| AC |
∵
| BD |
| AC |
| 1 |
| 2 |
| 3 |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
解得a=2，∴A（0，2）；
又∵2
| AE |
| EB |
| AE |
| 3 |
| 5 |
| AB |
设点E（x，y），∴（x，y-2）=
| 3 |
| 5 |
解得
|
| 3 |
| 5 |
| 4 |
| 5 |
∴
| CE |
| 8 |
| 5 |
| 4 |
| 5 |
| AB |
∴
| CE |
| AB |
| 8 |
| 5 |
| 4 |
| 5 |
故答案为：0．
点评：点评：本题考查了平面向量的应用问题，解题时应建立平面直角坐标系，利用向量的坐标运算解答共线和数量积，从而简化运算，是中档题．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
过双曲线
-
=1（a＞0，b＞0）的左顶点A作与实轴垂直的直线，交两渐近线于M、N两点，F为该双曲线的右焦点，若△FMN的内切圆恰好是x2+y2=a2，则该双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
设a，b是两条不同的直线，α，β是两个不同的平面（ ）
| A、若a∥b，a∥α，则b∥α |
| B、若a⊥b，a⊥α，b⊥β，则α⊥β |
| C、若α⊥β，a⊥β，则a∥α |
| D、若α∥β，a∥α，则a⊥β |
已知函数f（x）满足对所有的实数x，y，都有f（x）+f（2x+y）+5xy=f（3x-y）+2x2+1，则f（10）的值为（ ）
| A、-49 | B、-1 | C、0 | D、25 |
如图，三角形ABC中AB=3，AC=6，∠BAC=60°，D为BC中点，E为中线AD的中点．