题目内容
若某程序框图如图所示，则输出的n的值是（ ）
| A、3 | B、4 | C、5 | D、6 |
考点：程序框图
专题：算法和程序框图
分析：算法的功能是求满足P=1+3+…+（2n-1）＞20的最小n值，利用等差数列的前n项和公式求得P，根据P＞20，确定最小的n值．
解答：
解：由程序框图知：算法的功能是求满足P=1+3+…+（2n-1）＞20的最小n值，
∵P=1+3+…+（2n-1）=
×n=n2＞20，∴n≥5，
故输出的n=5．
故选：C．
∵P=1+3+…+（2n-1）=
| 1+2n-1 |
| 2 |
故输出的n=5．
故选：C．
点评：本题考查了循环结构的程序框图，根据框图的流程判断算法的功能是关键．
练习册系列答案
相关题目
现要制作一个圆锥形的漏斗，其母线长为l，要使其体积最大，高应为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
cos600°=（ ）
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
若曲线f（x）=ax2-lnx在点M（1，a）处的切线平行于x轴，则a的值为（ ）
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|
复数（1-i）2的虚部是（ ）
| A、-2i | B、2 | C、-2 | D、0 |
已知一个算法的程序框图如图所示，当输出的结果为0时，输入的x的值为（ ）
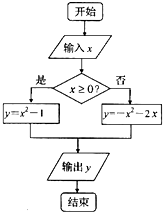
| A、-1或1 | B、-2或0 |
| C、-2或1 | D、-1或0 |
函数y=ln（x+2）在点（-1，0）处的切线方程为（ ）
| A、x+y+1=0 |
| B、x-y+1=0 |
| C、x-2y+1=0 |
| D、x+2y+1=0 |
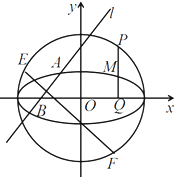如图，P是⊙O：x2+y2=4上任意一点，PQ⊥x轴，Q为垂足．设PQ的中点为M．