题目内容
给出定义:若m-
<x≤m+
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m.在此基础上给出下列关于函数f(x)=x-{x}的四个论断:
①f(-
)=
;②f(3.4)=-0.4
③f(-
)<f(
) ④y=f(x)的定义域为R,值域是[一
,
].
则其中论断正确的序号是( )
| 1 |
| 2 |
| 1 |
| 2 |
①f(-
| 1 |
| 2 |
| 1 |
| 2 |
③f(-
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
则其中论断正确的序号是( )
| A、①② | B、①③ | C、②④ | D、③④ |
考点:命题的真假判断与应用
专题:新定义,函数的性质及应用
分析:根据题意,画出函数f(x)的图象,结合函数的图象与解析式,对以下4个命题进行判断即可.
解答:
解:由题意x-{x}=x-m,
∴f(x)=x-{x}=x-m,
当m=0时,-
<x≤
,∴f(x)=x,
当m=1时,1-
<x≤1+
,f(x)=x-1;
当m=2时,2-
<x≤2+
,f(x)=x-2;
…;
画出函数的图象,如图所示;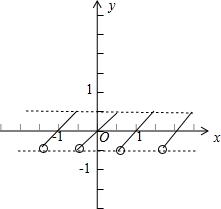
由图象知,①f(-
)=-
-(-1)=
,∴①正确;
②f(3.4)=3.4-3=0.4,∴②错误;
③f(x)在(-
,
]上是增函数,∴f(-
)<f(
),∴③正确;
④y=f(x)的定义域为R,值域是(-
,
],∴④错误;
综上,正确的命题是①③.
故选:B.
∴f(x)=x-{x}=x-m,
当m=0时,-
| 1 |
| 2 |
| 1 |
| 2 |
当m=1时,1-
| 1 |
| 2 |
| 1 |
| 2 |
当m=2时,2-
| 1 |
| 2 |
| 1 |
| 2 |
…;
画出函数的图象,如图所示;
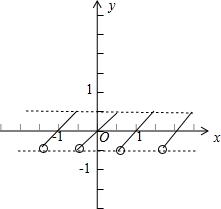
由图象知,①f(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②f(3.4)=3.4-3=0.4,∴②错误;
③f(x)在(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
④y=f(x)的定义域为R,值域是(-
| 1 |
| 2 |
| 1 |
| 2 |
综上,正确的命题是①③.
故选:B.
点评:本题考查了新定义的题目,解题的关键是读懂定义的内涵,尝试探究解决,是较难的题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)的图象如图所示,下列数值排序正确的是( )
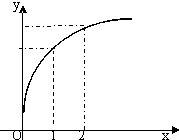

| A、0<f′(1)<f′(2)<f(2)-f(1) |
| B、0<f′(2)<f(2)-f(1)<f′(1) |
| C、0<f′(2)<f′(1)<f(2)-f(1) |
| D、0<f(2)-f(1)<f′(1)<f′(2) |
已知函数f(x)满足f(4)=5,且f(x)在R上的导数满足f′(x)-1<0,则不等式f(x2)<x2+1的解集为( )
| A、(-∞,-2)∪(2,+∞) |
| B、(2,+∞) |
| C、(2,+∞) |
| D、以上都不对 |
关于x的方程x2+(m-2)x+5-m=0的两根均大于2,则实数m的取值范围是( )
| A、(-5,-4] |
| B、(-∞,-5)∪(-5,-4) |
| C、(-∞,-4] |
| D、(-∞,-2) |
已知函数f(x)=sinx+cosx,则函数f(x)的一个单调递增区间为( )
A、(0,
| ||||
B、(
| ||||
C、(
| ||||
D、(
|
对于实数a和b,定义运算“*”:
,设f(x)=(2x-1)*(x-1),且关于x的方程f(x)=a(a∈R)恰有三个互不相等的实数根,则实数a的取值范围
是( )
|
是( )
A、(0,
| ||
B、[0,
| ||
C、[0,
| ||
D、(0,
|