题目内容
8.已知函数f(x)=tanx,x∈(0,$\frac{π}{2}$),若x1,x2∈(0,$\frac{π}{2}$),且x1≠x2(Ⅰ)用分析法证明:$\frac{1}{2}$[f(x1)+f(x2)]>f($\frac{{{x_1}+{x_2}}}{2}$);
(Ⅱ)借助图象,分析函数y1=ex,y2=lnx是否符合上述性质(无需证明).
分析 (Ⅰ)根据分析法的证明步骤证明:$\frac{1}{2}$[f(x1)+f(x2)]>f($\frac{{{x_1}+{x_2}}}{2}$);
(Ⅱ)作出函数y1=ex,y2=lnx的图象,即可得出结论.
解答 (Ⅰ)证明:∵$\frac{1}{2}$[f(x1)+f(x2)]=$\frac{1}{2}$(tanx1+tanx2)
=$\frac{1}{2}$($\frac{sin{x}_{1}}{cos{x}_{1}}$+$\frac{sin{x}_{2}}{cos{x}_{2}}$)=$\frac{sin({x}_{1}+{x}_{2})}{cos({x}_{1}+{x}_{2})+cos({x}_{1}-{x}_{2})}$,
又∵f($\frac{{{x_1}+{x_2}}}{2}$)=tan$\frac{{{x_1}+{x_2}}}{2}$=$\frac{sin({x}_{1}+{x}_{2})}{1+cos({x}_{1}+{x}_{2})}$,
欲证$\frac{1}{2}$[f(x1)+f(x2)]>f($\frac{{{x_1}+{x_2}}}{2}$),只需证$\frac{sin({x}_{1}+{x}_{2})}{cos({x}_{1}+{x}_{2})+cos({x}_{1}-{x}_{2})}$>$\frac{sin({x}_{1}+{x}_{2})}{1+cos({x}_{1}+{x}_{2})}$.
∵x1、x2∈(0,$\frac{π}{2}$),
∴sin(x1+x2)>0.
因此只需证cos(x1+x2)+cos(x1-x2)<1+cos(x1+x2),即证cos(x1-x2)<1.
∵x1、x2∈(0,$\frac{π}{2}$)且x1≠x2,
∴x1-x2∈(-$\frac{π}{2}$,$\frac{π}{2}$)且x1-x2≠0.
∴cos(x1-x2)<1成立.故原不等式成立.
(Ⅱ)解:y1=ex,如图所示:
具有上述性质;
y2=lnx,如图所示: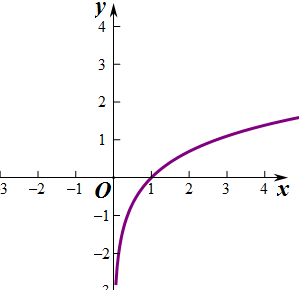
不具有上述性质.
点评 本题考查分析法证明不等式,考查函数的性质,考查数形结合的数学思想,属于中档题.

| A. | 不全相等 | B. | 都相等,且为$\frac{8}{59}$ | C. | 均不相等 | D. | 都相等,且为$\frac{1}{7}$ |
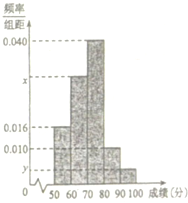 某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100)的有2人,由此推测频率分布直方图中的x=( )
某中学举行了一次“环保知识竞赛”活动,为了了解本次竞赛学生成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为n)进行统计,按照[50,60),[60,70),[70,80),[80,90),[90,100]的分组作出如图所示的频率分布直方图,但由于不慎丢失了部分数据.已知得分在[50,60)的有8人,在[90,100)的有2人,由此推测频率分布直方图中的x=( )| A. | 0.04 | B. | 0.03 | C. | 0.02 | D. | 0.01 |
| A. | (-∞,-$\frac{1}{2}$) | B. | (-∞,-$\frac{1}{2}$] | C. | (-∞,-2] | D. | (-∞,-2) |
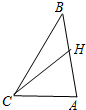 如图,在△ABC中,已知CA=2,CB=3,∠ACB=60°.
如图,在△ABC中,已知CA=2,CB=3,∠ACB=60°.