题目内容
用反证法证明“若△ABC的三边长a，b，c的倒数成等差数列，则B＜
”时，“假设”应为（ ）
| π |
| 2 |
A、B＜
| ||
B、B＞
| ||
C、B≤
| ||
D、B≥
|
考点：反证法与放缩法
专题：计算题,反证法
分析：考虑命题的反面，即可得出结论．
解答：
解：∵小于的反面是大于大于，
∴“假设”应为B≥
．
故选：D．
∴“假设”应为B≥
| π |
| 2 |
故选：D．
点评：此题主要考查了反证法的步骤，熟记反证法的步骤：（1）假设结论不成立；（2）从假设出发推出矛盾；（3）假设不成立，则结论成立．
练习册系列答案
阅读快车系列答案
相关题目
设等比数列{an}的前n项和为Sn．若q=2，S100=36，则a1+a3+…+a99=（ ）
| A、24 | B、12 | C、18 | D、22 |
若角α的终边上有一点P（a，a），a∈R且a≠0，则sinα的值是（ ）
A、
| ||||
B、-
| ||||
C、±
| ||||
| D、1 |
已知函数f（x-1）是偶函数，且x＜-1时，f′（x）＞0恒成立，又f（2）=0，则（x+1）f（x+2）＜0的解集为（ ）
| A、（-∞，-2）∪（4，+∞） |
| B、（-6，-1）∪（0，4） |
| C、（-6，-1）∪（0，+∞） |
| D、（-∞，-6）∪（4，+∞） |
已知向量
，
，
均为单位向量，且
⊥
，向量
，
与
的夹角分别为
，
，则|
+
+
|=（ ）
| a |
| b |
| c |
| a |
| b |
| b |
| a |
| c |
| π |
| 4 |
| 3π |
| 4 |
| a |
| b |
| c |
A、
| ||
| B、2 | ||
C、1+
| ||
| D、1 |
点M的直角坐标为（-
，-1）化为极坐标为（ ）
| 3 |
A、（2，
| ||
B、（2，
| ||
C、（2，
| ||
D、（2，
|
已知点F（-c，0）（c＞0）是双曲线
-
=1的左焦点，离心率为e，过F且平行于双曲线渐近线的直线与圆x2+y2=c2交于点P，且点P在抛物线y2=3cx上，则e2=（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如果θ=3rad，那么角θ的终边所在的象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
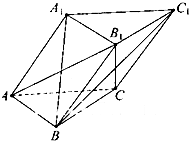已知三棱柱ABC-A1B1C1中，底面边长和侧棱长均为a，侧面A1ACC1⊥底面ABC，A1B=