题目内容
4．设点P是双曲线$\frac{x^2}{4}-{y^2}=1$上的点，F1，F2是其焦点，且∠F1PF2=90°，则△F1PF2的面积是（ ）| A． | 4 | B． | 5 | C． | 1 | D． | 2 |
分析 由条件可得||PF1|-|PF2||=2a，由题意可知△F1PF2为直角三角形利用勾股定理，结合双曲线的定义，即可求出△PF1F2的面积．
解答 解：由条件可得||PF1|-|PF2||=4，由题意可知△F1PF2为直角三角形，
设双曲线的焦距为2$\sqrt{5}$，则|PF1|2+|PF2|2=|F1F2|2=20，b2=1，
故（|PF1|-|PF2|）2+2|PF1|•|PF2|=|F1F2|2=20，即16+2|PF1|•|PF2|=20，
故|PF1|•|PF2|=2，
故△PF1F2的面积为$\frac{1}{2}$|PF1|•|PF2|=1．
故选：C．
点评 本题考查双曲线的定义与性质，考查三角形面积的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
的定义域是（ ）
B.
C.
D.
20．有一名同学家开了一个小卖部，他为了研究气温对某种引领销售的影响，记录了2015年7月至12月每月15号下午14时的气温和当天卖出的饮料杯数，得到如下资料：
该同学确定的研究方案是：先从这六组数据中选取2组，用剩下的4组数据求线性回归方程，再用被选中的2组数据进行检验．
（1）求选取2组数据恰好是相邻的两个月的概率；
（2）若选中的是8月与12月的两组数据，根据剩下的4组数据，求出y关于x的线性回归方程$\hat y=bx+\hat a$．
附：对于一组数据（x1，y1），（x2，y2），…，（xn，yn），其回归直线$\hat a=\overline y-\hat b\overline x$的斜率和截距的最小二乘估计分别为：$b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．
| 日期 | 7月15日 | 8月15日 | 9月15日 | 10月15日 | 11月15日 | 12月15日 |
| 摄氏温度x（℃） | 36 | 35 | 30 | 24 | 18 | 8 |
| 饮料杯数y | 27 | 29 | 24 | 18 | 15 | 5 |
（1）求选取2组数据恰好是相邻的两个月的概率；
（2）若选中的是8月与12月的两组数据，根据剩下的4组数据，求出y关于x的线性回归方程$\hat y=bx+\hat a$．
附：对于一组数据（x1，y1），（x2，y2），…，（xn，yn），其回归直线$\hat a=\overline y-\hat b\overline x$的斜率和截距的最小二乘估计分别为：$b=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2-n{{\overline x}^2}}}}$，$\hat a=\overline y-\hat b\overline x$．
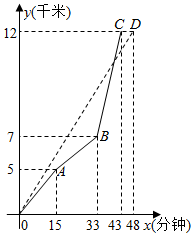如图，在一次自行车越野赛中，甲，乙两名选手所走的路程y（千米）随时间x（分钟）变化的图象（全程）分别用实线（O→A→B→C）与虚线（ OD）表示，那么，在本次比赛过程中，乙领先甲时的x的取值范围是0＜x＜38．
15．设函数f（x）=$\left\{\begin{array}{l}{{2}^{x}-1，x≥1}\\{1，x＜1}\end{array}\right.$，则不等式f（6-x2）＞f（x）的解集为（ ）
| A． | （-3，1） | B． | （-2，1） | C． | （-$\sqrt{5}$，2） | D． | （-2，$\sqrt{5}$） |