题目内容
17.求下列极限:(1)$\underset{lim}{x→1}$$\sqrt{{x}^{2}+2}$;
(2)$\underset{lim}{x→\frac{π}{4}}$(sinx-cosx);
(3)$\underset{lim}{x→1}$cos lnx;
(4)$\underset{lim}{x→0}$esinx.
分析 分析各个函数都是连续函数,求解极限,代入即求解.
解答 解:(1)$\underset{lim}{x→1}$$\sqrt{{x}^{2}+2}$=$\sqrt{3}$
(2)$\underset{lim}{x→\frac{π}{4}}$(sinx-cosx)=$\frac{\sqrt{2}}{2}$$-\frac{\sqrt{2}}{2}$=0;
(3)$\underset{lim}{x→1}$cos lnx=cosln1=cos0=1;
(4)$\underset{lim}{x→0}$esinx=esin0=e0=1.
点评 本题简单的考查了函数与极限的运算,理解连续函数的极限的求解即可.

练习册系列答案
相关题目
6.直线y=k(x+1)(k∈R)与不等式组$\left\{\begin{array}{l}2x+y-2≤0\\ 2x-y-2≤0\\ x≥0\end{array}\right.$?,表示的平面区域有公共点,则k的取值范围是( )
| A. | [-2,2] | B. | (-∞,-2]∪[2,+∞) | C. | [-$\frac{1}{2}$,$\frac{1}{2}$] | D. | (-∞,-$\frac{1}{2}$]∪[$\frac{1}{2}$,+∞) |
4.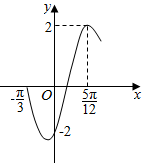 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )
 函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )
函数f(x)=2sin(ωx+φ)(ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则ω,φ的值分别是( )| A. | $2\;,\;-\frac{π}{3}$ | B. | $2\;,\;-\frac{π}{6}$ | C. | $4\;,\;-\frac{π}{6}$ | D. | $4\;,\;\frac{π}{3}$ |
 的解集是 .
的解集是 . 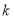 ,直线
,直线 与圆
与圆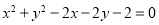 的位置关系是________
的位置关系是________ 某电子商务公司随机抽取l 000名网络购物者进行调查.这1000名购物者2015年网上购物金额(单位:万元)均在区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),[0.5,0.6),[0.6,0.7),[0.7,0.8),[0.8,0.9].购物金额的频率分布直方图如下:
某电子商务公司随机抽取l 000名网络购物者进行调查.这1000名购物者2015年网上购物金额(单位:万元)均在区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),[0.5,0.6),[0.6,0.7),[0.7,0.8),[0.8,0.9].购物金额的频率分布直方图如下: