题目内容
从6人中选4人分别去北京，上海，广州，重庆四个城市游览，每人只去一个城市游览，但甲，乙两人都不去北京，则不同的选择方案有（ ）
| A、300种 | B、240种 |
| C、144种 | D、96种 |
考点：排列、组合及简单计数问题
专题：概率与统计
分析：由于甲，乙两人都不去北京，故先安排北京的游览方法，再安排其余3个城市的游览方法，根据分步计数原理得到结果．
解答：
解：先安排北京的游览方法，有4种，再安排上海的游览方法，有5种，
再安排广州的游览方法，有4种，再安排重庆的游览方法，有3种．
根据分步计数原理，不同的选择方案有4×5×4×3=240种，
故选B．
再安排广州的游览方法，有4种，再安排重庆的游览方法，有3种．
根据分步计数原理，不同的选择方案有4×5×4×3=240种，
故选B．
点评：本题考查分步计数问题，解题时一定要分清做这件事需要分为几步，每一步包含几种方法，看清思路，把几个步骤中数字相乘得到结果，属于中档题．
练习册系列答案
相关题目
一袋中装有5只球，编号为1，2，3，4，5，在袋中同时取3只，以ξ表示取出的三只球中的最小号码，则P（ξ=2）=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
| lim |
| △x→0 |
| f(x0+△x)-f(x0) |
| △x |
| A、恒取正值或恒取负值 |
| B、有时可以取0 |
| C、恒取正值 |
| D、可以取正值和负值，但不能取0 |
不等式（x2-4）（x-6）2≤0的解集为（ ）
| A、{x|-2≤x≤2} |
| B、{x|x≥2或x≤-2} |
| C、{x|-2≤x≤2或x=6} |
| D、{x|x≥2} |
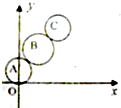我们把圆心在一条直线上且相邻两圆彼此外切的一组圆 叫做“串圆”．在如图所示的“串圆”中，⊙A和⊙C的方程分别为x2+（y-1）2=2和（x-6）2+（y-7）2=2，则⊙B的方程为