题目内容
旅游公司为4个旅游团提供5条旅游线路，每个旅游团任选其中一条．
（1）求4个旅游团选择互不相同的线路共有多少种方法；
（2）求恰有2条线路被选中的概率．
（1）求4个旅游团选择互不相同的线路共有多少种方法；
（2）求恰有2条线路被选中的概率．
考点：等可能事件的概率
专题：计算题,概率与统计
分析：（1）利用排列知识，可得4个旅游团选择互不相同的线路方法；
（2）由题意每个旅游团选择那个线路是等可能的，故总的选法有54种，确定事件“恰有2条线路被选中”的选法种数，即可求出恰有2条线路被选中的概率．
（2）由题意每个旅游团选择那个线路是等可能的，故总的选法有54种，确定事件“恰有2条线路被选中”的选法种数，即可求出恰有2条线路被选中的概率．
解答：
解：（1）4个旅游团选择互不相同的线路共有
=120种方法；
（2）由题意每个旅游团选择那个线路是等可能的，故总的选法有54种，
又事件“恰有2条线路被选中”的选法种数是
(24-2)，
∴P=
=
．
| A | 4 5 |
（2）由题意每个旅游团选择那个线路是等可能的，故总的选法有54种，
又事件“恰有2条线路被选中”的选法种数是
| C | 2 5 |
∴P=
| ||
| 54 |
| 28 |
| 125 |
点评：本题考查等可能事件的概率，解题的关键是求出事件所包含的基本事件数与总的基本事件数，再由公式求出概率．
练习册系列答案
相关题目
已知点A（a，b），B（x，y）为抛物线y=x2上两点，且x＞a，记|AB|=g（x）．若函数g（x）在定义域（a，+∞）上单调递增，则点A的坐标不可能是（ ）
| A、（1，1） |
| B、（0，0） |
| C、（-1，1） |
| D、（-2，4） |
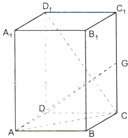如图，长方体ABCD-A1B1C1D1中，AB=AD=1，AA1=2，G是CC1上的动点．