题目内容
已知圆P:x2+y2-4x+2y-3=0和圆外一点M(4,-8).过点M作圆的割线交圆于A,B两点,若|AB|=4,求直线AB的方程: .
考点:直线与圆相交的性质
专题:直线与圆
分析:由条件求得圆心P(2,-1)到直线AB的距离等于2,用点斜式设出设AB的方程,由弦心距d=
=2,求得k的值,可得直线AB的方程.
| |2k+1-4k-8| | ||
|
解答:
解:当直线斜率不存在时,直线方程为x=4,代入圆P:x2+y2-4x+2y-3=0,解得y=-3,1,此时弦长为4,符合题意;
当直线斜率存在时,圆P:x2+y2-4x+2y-3=0,即( x-2)2+(y+1)2=8,由于弦长AB=4,
可得弦心距d=
=2,即圆心P(2,-1)到直线AB的距离等于2.
设AB的方程为y+8=k(x-4),即 kx-y-4k-8=0,由d=
=2,求得k=-
,
故AB的方程为 45x+28y+44=0,
综上,符合条件的直线方程为45x+28y+44=0或x=4,
故答案为:45x+28y+44=0或x=4.
当直线斜率存在时,圆P:x2+y2-4x+2y-3=0,即( x-2)2+(y+1)2=8,由于弦长AB=4,
可得弦心距d=
| 8-22 |
设AB的方程为y+8=k(x-4),即 kx-y-4k-8=0,由d=
| |2k+1-4k-8| | ||
|
| 45 |
| 28 |
故AB的方程为 45x+28y+44=0,
综上,符合条件的直线方程为45x+28y+44=0或x=4,
故答案为:45x+28y+44=0或x=4.
点评:本题主要考查直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,用点斜式求直线的方程,属于基础题.

练习册系列答案
相关题目
若平面向量
与
=(1,-2)的夹角是180°,且|
|=3
,则
等于( )
| a |
| b |
| a |
| 5 |
| a |
| A、.(6,-3) |
| B、(3,-6) |
| C、(-3,6) |
| D、(-6,3) |
点M与定点F(4,0)的距离和它到定直线x=
的距离之比是常数
,则M的轨迹方程为( )
| 25 |
| 4 |
| 4 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知函数f(x),g(x)分别是定义在R上的奇函数与偶函数,且f(x)=g(x-1),则g(2015)=( )
| A、0 | B、1 |
| C、2014 | D、2015 |
已知函数f(x)=
在R上 单调递减,那么实数a的取 值范围是( )
|
| A、(0,1) | ||||
B、(0,
| ||||
C、(
| ||||
D、(
|
下列四组函数中,其函数图象相同的是( )
A、y=x,y=
| |||||
B、y=|x|,y=
| |||||
| C、y=log2x,y=log4x2 | |||||
D、y=
|
如果等差数列{an}中,a3+a4+a5=12,那么a4等于( )
| A、4 | B、2 | C、6 | D、12 |
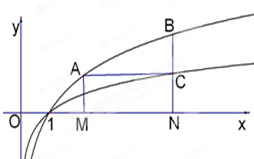 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点c,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点c,且AC与x轴平行.