题目内容
已知点M是曲线y=
x2+1上一动点,且点M为线段OP的中点,则动点P的轨迹方程为 .
| 1 |
| 2 |
考点:轨迹方程
专题:圆锥曲线的定义、性质与方程
分析:设出P的坐标,求出M的坐标,动点M在抛物线y=
x2+1上运动,点M满足抛物线方程,代入求解,即可得到P的轨迹方程.
| 1 |
| 2 |
解答:
解:设P的坐标(x,y),由题意点M为线段OP的中点,可知M(
,
),
动点M在抛物线y=
x2+1上运动,所以
=
(
)2+1,所以y=
x2+2
动点P的轨迹方程为:y=
x2+2.
故答案为:y=
x2+2.
| x |
| 2 |
| y |
| 2 |
动点M在抛物线y=
| 1 |
| 2 |
| y |
| 2 |
| 1 |
| 2 |
| x |
| 2 |
| 1 |
| 4 |
动点P的轨迹方程为:y=
| 1 |
| 4 |
故答案为:y=
| 1 |
| 4 |
点评:本题是中档题,考查点的轨迹方程的求法,相关点法,是常见的求轨迹方程的方法,注意中点坐标的应用.

练习册系列答案
相关题目
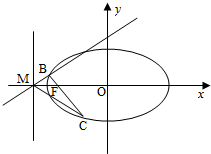 如图,已知椭圆W:
如图,已知椭圆W: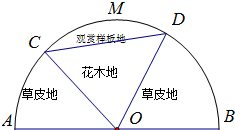 某园林公司计划在一块O为圆心,R(R为常数)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.
某园林公司计划在一块O为圆心,R(R为常数)为半径的半圆形(如图)地上种植花草树木,其中弓形CMDC区域用于观赏样板地,△OCD区域用于种植花木出售,其余区域用于种植草皮出售.已知观赏样板地的成本是每平方米2元,花木的利润是每平方米8元,草皮的利润是每平方米3元.