题目内容
3.已知$\overline z$是z的共轭复数,若$\overline z+z=2,(\overline z-z)i=2$(其中i为虚数单位),则z的值为( )| A. | 1-i | B. | -1-i | C. | -1+i | D. | 1+i |
分析 设z=a+bi(a,b∈R),结合已知列关于a,b的方程组求解.
解答 解:设z=a+bi(a,b∈R),则$\overline{z}=a-bi$,
由$\overline z+z=2,(\overline z-z)i=2$,得
$\left\{\begin{array}{l}{2a=2}\\{-2b{i}^{2}=2}\end{array}\right.$,解得a=1,b=1.
∴z=1+i.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数相等的条件,是基础的计算题.

练习册系列答案
相关题目
11.某四棱锥的三视图如图所示,其俯视图为等腰直角三角形,则该四棱锥的体积为( )
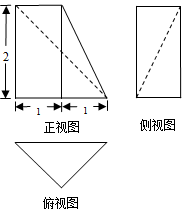

| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{4}{3}$ | D. | $\sqrt{2}$ |
18.已知等差数列{an}的前n项和为Sn,且2S3-3S2=15,则数列{an}的公差为( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
15.已知$sin(α+\frac{π}{6})=\frac{1}{3}$,则$cos(2α-\frac{2π}{3})$的值是( )
| A. | $\frac{5}{9}$ | B. | $-\frac{8}{9}$ | C. | $-\frac{1}{3}$ | D. | $-\frac{7}{9}$ |
12.命题“$?{x_0}∈R,{2^{x_0}}≤0$”的否定是( )
| A. | 不存在${x_0}∈R,{2^{x_0}}>0$ | B. | ?x∈R,2x>0 | ||
| C. | $?{x_0}∈R,{2^{x_0}}≥0$. | D. | ?x∈R,2x≤0 |
