题目内容
11.已知$z=-\frac{1}{2}+\frac{{\sqrt{3}i}}{2}$.(1)$\bar z$是z的共轭复数,求${\bar z^2}+\bar z+1$的值;
(2)类比数列的有关知识,求${S_{2016}}=1+z+{z^2}+…+{z^{2015}}$的值.
分析 (1)利用复数的乘法与加减运算法则化简求解即可.
(2)利用数列的求和,直接求解化简即可.
解答 解:(1)$\overline{z}=-\frac{1}{2}-\frac{{\sqrt{3}i}}{2}$,${\bar z^2}+\bar z+1={({-\frac{1}{2}-\frac{{\sqrt{3}i}}{2}})^2}-\frac{1}{2}-\frac{{\sqrt{3}i}}{2}+1=0$
(2)${S_{2016}}=1+z+{z^2}+…+{z^{2015}}=\frac{{1×({1-{z^{2016}}})}}{1-z}$,
∵${z^3}={({-\frac{1}{2}+\frac{{\sqrt{3}i}}{2}})^3}=1$,
∴1-z2016=1-(z3)672=1-1=0,
∴${S_{2016}}=1+z+{z^2}+…+{z^{2015}}=\frac{{1×({1-{z^{2016}}})}}{1-z}=0$.
点评 本题考查复数的基本运算,数列求和,考查计算能力.

练习册系列答案
相关题目
16.下列函数是奇函数的是( )
| A. | f(x)=x4 | B. | $f(x)=x+\frac{1}{x}$ | C. | f(x)=x3-1 | D. | $f(x)=\frac{1}{x^2}$ |
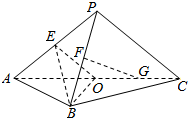 如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.
如图,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.