题目内容
15.设双曲线$\frac{x^2}{3}-{y^2}$=1的两焦点分别为F1,F2,P为双曲线上的一点,若PF1与双曲线的一条渐近线平行,则$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=( )| A. | $-\frac{35}{12}$ | B. | $-\frac{11}{12}$ | C. | $-\frac{7}{12}$ | D. | $-\frac{1}{12}$ |
分析 求得双曲线的a,b,c,可得两焦点的坐标和渐近线方程,可设PF1与直线$y=\frac{{\sqrt{3}}}{3}x$平行,求得平行线的方程代入双曲线的方程,求得P的坐标,再由向量的数量积的坐标表示,计算即可得到所求值.
解答 解:由双曲线$\frac{x^2}{3}-{y^2}$=1的a=$\sqrt{3}$,b=1,c=2,
得F1(-2,0),F2(2,0),
渐近线为$y=±\frac{{\sqrt{3}}}{3}x$,
由对称性,不妨设PF1与直线$y=\frac{{\sqrt{3}}}{3}x$平行,
可得${l_{P{F_1}}}:y=\frac{{\sqrt{3}}}{3}({x+2})$,
由$\left\{{\begin{array}{l}{\frac{x^2}{3}-{y^2}=1}\\{y=\frac{{\sqrt{3}}}{3}({x+2})}\end{array}}\right.$得$P({-\frac{7}{4},\frac{{\sqrt{3}}}{12}})$,
即有$\overrightarrow{P{F_1}}=({-\frac{1}{4},-\frac{{\sqrt{3}}}{12}})$,$\overrightarrow{P{F_2}}=({\frac{15}{4},-\frac{{\sqrt{3}}}{12}})$,
$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$=-$\frac{1}{4}$×$\frac{15}{4}$+(-$\frac{\sqrt{3}}{12}$)2=-$\frac{11}{12}$.
故选B.
点评 本题考查向量的数量积的坐标表示,注意运用双曲线的渐近线方程和两直线平行的条件,以及联立直线和双曲线求交点,考查运算能力,属于中档题.

| A. | $\frac{{y}^{2}}{2}$-$\frac{{x}^{2}}{3}$=1 | B. | $\frac{{y}^{2}}{4}$-x2=1 | C. | y2-$\frac{{x}^{2}}{4}$=1 | D. | $\frac{{y}^{2}}{3}$-$\frac{{x}^{2}}{2}$=1 |
| A. | [-1,1)∪(2,3) | B. | [-1,1]∪[2,3) | C. | (1,2) | D. | (-∞,+∞) |
| A. | 1+2i | B. | 1-2i | C. | -1+2i | D. | -1-2i |
| A. | 充要 | B. | 必要不充分 | ||
| C. | 充分不必要 | D. | 既不充分又不必要 |
| A. | -3 | B. | $-\frac{1}{2}$ | C. | 3 | D. | 6 |
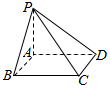 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AB=1,当直线PD与平面PBC所成角的正弦值最大时,该几何体的外接球的体积为$\frac{\sqrt{3}π}{2}$.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PA⊥平面ABCD,AB=1,当直线PD与平面PBC所成角的正弦值最大时,该几何体的外接球的体积为$\frac{\sqrt{3}π}{2}$.