题目内容
在△ABC中,内角A,B,C所对的边分别为a,b,c.已知cosB(tanAtanB+tanCtanB)=tanAtanC,
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
(1)求证:a,b,c成等比数列;
(2)若a=1,c=2,求△ABC的面积S.
考点:等比关系的确定,同角三角函数基本关系的运用,余弦定理
专题:等差数列与等比数列,解三角形
分析:(1)根据同角的三角函数的关系式将条件进行化简,结合正弦定理和余弦定理,以及等比数列的定义即可证明a,b,c成等比数列;
(2)根据条件求出b,结合余弦定理求出cosB,利用三角形的面积公式即可求△ABC的面积S.
(2)根据条件求出b,结合余弦定理求出cosB,利用三角形的面积公式即可求△ABC的面积S.
解答:
(1)证明:由cosB(tanAtanB+tanCtanB)=tanAtanC,
得cosB(
+
)=
,
即
+
=
,
则sinAsinBcosC+cosAsinBsinC=sinAsinC,
由正弦定理和余弦定理得ab•
+bc•
=ac,
即a2+b2-c2+b2+c2-a2=2ac,
则2b2=2ac,
即b2=ac,故a,b,c成等比数列.
(2)∵b2=ac,
∴当a=1,c=2时,b2=ac=2,即b=
,
cosB=
=
=
,
∴sinB=
=
,
则三角形的面积S=
acsinB=
×1×2×
=
.
得cosB(
| sinAsinB |
| cosAcosB |
| sinCsinB |
| cosBcosC |
| sinCsinA |
| cosAcosC |
即
| sinAsinB |
| cosA |
| sinCsinB |
| cosC |
| sinCsinA |
| cosAcosC |
则sinAsinBcosC+cosAsinBsinC=sinAsinC,
由正弦定理和余弦定理得ab•
| a2+b2-c2 |
| 2ab |
| b2+c2-a2 |
| 2bc |
即a2+b2-c2+b2+c2-a2=2ac,
则2b2=2ac,
即b2=ac,故a,b,c成等比数列.
(2)∵b2=ac,
∴当a=1,c=2时,b2=ac=2,即b=
| 2 |
cosB=
| a2+c2-b2 |
| 2ac |
| 1+4-2 |
| 2×1×2 |
| 3 |
| 4 |
∴sinB=
1-(
|
| ||
| 4 |
则三角形的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
点评:本题主要考查等比数列的判断,以及正弦定理和余弦定理的应用,考查学生的计算能力.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
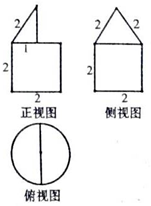
某几何体的三视图如图所示,则该几何体的体积是( )

A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(
|