题目内容
3.设△ABC内角A,B,C所对的边分别为a,b,c,且$ccosB=\sqrt{3}bsinC$.(1)若${a^2}sinC=4\sqrt{3}sinA$,求△ABC的面积;
(2)若$a=2\sqrt{3}$,$b=\sqrt{7}$,且c>b,BC边的中点为D,求AD的长.
分析 (1)由题意和正弦定理以及同角三角函数基本关系可得tanB,可得B值,再由正弦定理整体可得ac的值,代入三角形的面积公式计算可得;
(2)由余弦定理可得c值,在△ABD中由余弦定理可得.
解答 解:(1)∵在△ABC中$ccosB=\sqrt{3}bsinC$,
∴由正弦定理可得sinCcosB=$\sqrt{3}$sinBsinC,
约掉sinC可得cosB=$\sqrt{3}$sinB,
∴tanB=$\frac{sinB}{cosB}$=$\frac{\sqrt{3}}{3}$,B=$\frac{π}{6}$,
又∵${a^2}sinC=4\sqrt{3}sinA$,
∴a2c=4$\sqrt{3}$a,∴ac=4$\sqrt{3}$,
∴△ABC的面积S=$\frac{1}{2}$acsinB=$\sqrt{3}$;
(2)∵$a=2\sqrt{3}$,$b=\sqrt{7}$,
∴由余弦定理可得7=12+c2-2×2$\sqrt{3}$×$\frac{\sqrt{3}}{2}$c,
解关于c的方程可得c=5,或c=1(不满足c>b,舍去)
∵BC边的中点为D,∴在△ABD中由余弦定理可得:
AD2=($\sqrt{3}$)2+52-2×$\sqrt{3}$×5×$\frac{\sqrt{3}}{2}$=13,
开方可得AD的长为$\sqrt{13}$.
点评 本题考查正余弦定理解三角形,涉及整体法和三角形的面积公式,属中档题.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
8.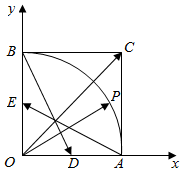 如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
 如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )
如图,在直角坐标平面中正方形OACB的边长为1,点P为扇形,OAB的弧$\widehat{AB}$上任意一点,D为OA的中点,E为OB的中点,$\overrightarrow{OP}$=x$\overrightarrow{AE}$+y$\overrightarrow{BD}$(x,y∈R),设$\overrightarrow{a}$=(x,y),则$\overrightarrow{a}$•$\overrightarrow{OC}$的最大值为( )| A. | -$\sqrt{2}$ | B. | -2 | C. | -$\sqrt{3}$ | D. | -2$\sqrt{2}$ |
11.a,b表示不同的直线,α,β,γ表示不同的平面.
①若α∩β=a,b?α,a⊥b,则α⊥β;
②若a?α,a垂直于β内任意一条直线,则α⊥β;
③若α⊥β,α∩β=a,α∩γ=b,则a⊥b;
④若a不垂直平面α,则a不可能垂直于平面α内的无数条直线;
⑤若a⊥α,b⊥β,a∥b,则α∥β.
上述五个命题中,正确命题的序号是( )
①若α∩β=a,b?α,a⊥b,则α⊥β;
②若a?α,a垂直于β内任意一条直线,则α⊥β;
③若α⊥β,α∩β=a,α∩γ=b,则a⊥b;
④若a不垂直平面α,则a不可能垂直于平面α内的无数条直线;
⑤若a⊥α,b⊥β,a∥b,则α∥β.
上述五个命题中,正确命题的序号是( )
| A. | ①②③ | B. | ②④⑤ | C. | ④⑤ | D. | ②⑤ |
15.为得到函数y=cos(2x+$\frac{π}{3}$)的图象,只需将函数y=sin2x的图象( )
| A. | 向左平移$\frac{5π}{12}$个单位长度 | B. | 向右平移$\frac{5π}{12}$个单位长度 | ||
| C. | 向左平移$\frac{5π}{6}$个单位长度 | D. | 向右平移$\frac{5π}{6}$个单位长度 |