题目内容
在△ABC中,AB=3,∠A=60°,∠A的平分线AD交边BC于点D,且
=
+λ
(λ∈R),则AD的长为 .
| AD |
| 2 |
| 3 |
| AC |
| AB |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:如图所示,过点D作DE∥AB,DF∥AC分别交AC,AB于点E,F.由于
=
,可得
=
=
,可得AC,λ=
.即
=
+
.再利用数量积的运算性质即可得出.
| AE |
| AC |
| 2 |
| 3 |
| BD |
| BC |
| BF |
| BA |
| 2 |
| 3 |
| 1 |
| 3 |
| AD |
| 2 |
| 3 |
| AC |
| 1 |
| 3 |
| AB |
解答:
解:如图所示,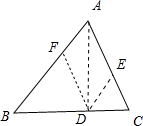
过点D作DE∥AB,DF∥AC分别交AC,AB于点E,F.
∵
=
,∴
=
=
,
∴AF=
AB,
=
=
,
∴λ=
.
∴
=
+
.
∵AB=3,可得AC=
.
∵∠A=60°,
∴
•
=
×3×cos60°=
.
∴
2=
2+
2+
•
=3,
∴|
|=
.
故答案为:
.

过点D作DE∥AB,DF∥AC分别交AC,AB于点E,F.
∵
| AE |
| AC |
| 2 |
| 3 |
| BD |
| BC |
| BF |
| BA |
| 2 |
| 3 |
∴AF=
| 1 |
| 3 |
| AB |
| AC |
| BD |
| DC |
| 2 |
| 1 |
∴λ=
| 1 |
| 3 |
∴
| AD |
| 2 |
| 3 |
| AC |
| 1 |
| 3 |
| AB |
∵AB=3,可得AC=
| 3 |
| 2 |
∵∠A=60°,
∴
| AC |
| AB |
| 3 |
| 2 |
| 9 |
| 4 |
∴
| AD |
| 4 |
| 9 |
| AC |
| 1 |
| 9 |
| AB |
| 4 |
| 9 |
| AB |
| AC |
∴|
| AD |
| 3 |
故答案为:
| 3 |
点评:本题考查了向量的平行四边形法则、三角形内角平分线定理、数量积的运算性质,考查了推理能力和计算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目