题目内容
已知:函数f(x)=sinx-cos2x+a.
(1)求函数f(x)的最值;
(2)当a为何值时,方程f(x)=0在区间[0,2π)有两解?
(3)求函数f(x)在区间[0,2π]上的单调递增区间.
(1)求函数f(x)的最值;
(2)当a为何值时,方程f(x)=0在区间[0,2π)有两解?
(3)求函数f(x)在区间[0,2π]上的单调递增区间.
考点:三角函数的最值,正弦函数的单调性
专题:三角函数的图像与性质
分析:(1)首先,化简函数解析式得到f(x)═(sinx+
)2-
+a,然后,结合sinx∈[-1,1]进行求解;
(2)换元法,得到t2+t+a-1=0在区间(-1,1)上有一解令g(t)=t2+t+a-1,从而有
或△=0,然后,求解即可;
(3)结合三角函数的单调性求解单调区间即可.
| 1 |
| 2 |
| 5 |
| 4 |
(2)换元法,得到t2+t+a-1=0在区间(-1,1)上有一解令g(t)=t2+t+a-1,从而有
|
(3)结合三角函数的单调性求解单调区间即可.
解答:
解(1)由f(x)=sinx-cos2x+a=sinx-(1-sin2x)+a=(sinx+
)2-
+a,
∵sinx∈[-1,1],
所以当sinx=1时f(x)max=1+a,
当sinx=-
时f(x)min=a-
∴函数f(x)的最大值为a+1,最小值为a-
.
(2)由f(x)=0,
∴sinx-cos2x+a=0,
∴sinx-(1-sin2x)+a=0,
令t=sinx,∵x∈[0,2π),
∴t∈[-1,1],
要使方程f(x)=0在区间[0,2π)有两解,
有t2+t+a-1=0在区间(-1,1)上有一解令g(t)=t2+t+a-1,
∴
或△=0,
∴a∈(-1,1)或a=
∴a的取值范围是(-1,1)∪{
}.
(3)由f(x)=sinx-cos2x+a
=sinx-(1-sin2x)+a
=(sinx+
)2-
+a,
令t=sinx,
∵x∈[0,2π],
∴t∈[-1,1],
∴y=(t+
)2-
+a在[-1,-
]上单调递减,在[-
,1]上单调递增
当t∈[-1,-
]时,
x∈[
,
],
而t=sinx在[
,
]上单调递减,在[
,
]上单调递增,
所以当x∈[
,
]时f(x)单调递增,
当t∈[-
,1]时,
x∈[0,
]∪[
,2π] 而t=sinx在x∈[0,
],x∈[
,2π]时单调递增,
∴f(x)在[0,
],[
,2π]上单调递增.
综上函数f(x)在区间[0,2π]上的单调递增区间为[0,
],[
,
],[
,2π].
| 1 |
| 2 |
| 5 |
| 4 |
∵sinx∈[-1,1],
所以当sinx=1时f(x)max=1+a,
当sinx=-
| 1 |
| 2 |
| 5 |
| 4 |
∴函数f(x)的最大值为a+1,最小值为a-
| 5 |
| 4 |
(2)由f(x)=0,
∴sinx-cos2x+a=0,
∴sinx-(1-sin2x)+a=0,
令t=sinx,∵x∈[0,2π),
∴t∈[-1,1],
要使方程f(x)=0在区间[0,2π)有两解,
有t2+t+a-1=0在区间(-1,1)上有一解令g(t)=t2+t+a-1,
∴
|
∴a∈(-1,1)或a=
| 5 |
| 4 |
∴a的取值范围是(-1,1)∪{
| 5 |
| 4 |
(3)由f(x)=sinx-cos2x+a
=sinx-(1-sin2x)+a
=(sinx+
| 1 |
| 2 |
| 5 |
| 4 |
令t=sinx,
∵x∈[0,2π],
∴t∈[-1,1],
∴y=(t+
| 1 |
| 2 |
| 5 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
当t∈[-1,-
| 1 |
| 2 |
x∈[
| 7π |
| 6 |
| 11π |
| 6 |
而t=sinx在[
| 7π |
| 6 |
| 3π |
| 2 |
| 3π |
| 2 |
| 11π |
| 6 |
所以当x∈[
| 7π |
| 6 |
| 3π |
| 2 |
当t∈[-
| 1 |
| 2 |
x∈[0,
| 7π |
| 6 |
| 11π |
| 6 |
| π |
| 2 |
| 11π |
| 6 |
∴f(x)在[0,
| π |
| 2 |
| 11π |
| 6 |
综上函数f(x)在区间[0,2π]上的单调递增区间为[0,
| π |
| 2 |
| 7π |
| 6 |
| 3π |
| 2 |
| 11π |
| 6 |
点评:本题重点考查了三角函数的图象与性质、三角恒等变换等知识,属于中档题.

练习册系列答案
相关题目
函数f(x)=2x-
-m的一个零点在区间(1,3)内,则实数m的取值范围是( )
| 3 |
| x |
| A、(-1,7) |
| B、(0,5) |
| C、(-7,1) |
| D、(1,5) |
已知定义在(-1,1)上的函数f (x),其导函数为f′(x)=l+cosx,且f(0)=0,如果f(1-x)+f(l-x2)<0,则实数x的取值范围为( )
| A、(0,1) | ||||
B、(1,
| ||||
C、(-2,-
| ||||
D、(1,
|
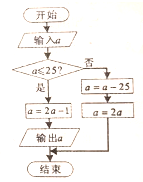 某班有49位同学玩“数字接龙”游戏,具体规则按如图所示的程序框图执行(其中a为座位号),并以输出的值作为下一个输入的值,若第一次 输入的值为8,则第三次输出的值为( )
某班有49位同学玩“数字接龙”游戏,具体规则按如图所示的程序框图执行(其中a为座位号),并以输出的值作为下一个输入的值,若第一次 输入的值为8,则第三次输出的值为( )