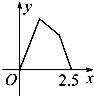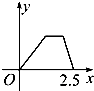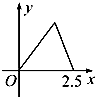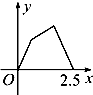题目内容
已知函数f(x)=a2x+2ax-1(a>0,且a≠1)在区间[-1,1]上的最大值为14,求实数a的值.
考点:函数的最值及其几何意义
专题:函数的性质及应用
分析:先令t=ax,转化为二次函数,再结合a>1或0<a<1确定出t的范围,结合单调性确定何时取最大值列出方程即可.
解答:
解:令t=ax>0
则原函数化为y=t2+2t-1=(t+1)2-2
结合二次函数的图象与性质可知该函数在(0,+∞)上是单调增函数
结合x∈[-1,1],
则当a>1时,t=ax∈[
,a],所以ymax=a2+2a-1=14,解得a=3或-5(舍),所以此时a=3符合题意;
当0<a<1时,t=ax∈[a,
],所以ymax=(
)2+
-1=14,解得
=3或-5(舍),故a=
符合题意;
综上,所求实数a的值为3或
.
则原函数化为y=t2+2t-1=(t+1)2-2
结合二次函数的图象与性质可知该函数在(0,+∞)上是单调增函数
结合x∈[-1,1],
则当a>1时,t=ax∈[
| 1 |
| a |
当0<a<1时,t=ax∈[a,
| 1 |
| a |
| 1 |
| a |
| 2 |
| a |
| 1 |
| a |
| 1 |
| 3 |
综上,所求实数a的值为3或
| 1 |
| 3 |
点评:本题考查了利用指数函数与二次函数的单调性求最值,利用换元法将问题转化为二次函数的问题是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面上,已知
⊥
,|
|=|
|=1,
=
+
,若|
|<
,则|
|的取值范围是( )
| AB1 |
| AB2 |
| OB1 |
| OB2 |
| AP |
| AB1 |
| AB2 |
| OP |
| 1 |
| 2 |
| OA |
A、(0,
| ||||||||
B、(
| ||||||||
C、(
| ||||||||
D、(
|
已知函数f(x)=|x2+2x-3|,若关于x的方程f2(x)-(a+2)f(x)+a2-2a=0有5个不等实根,则实数a值是( )
| A、2 | B、4 | C、2或4 | D、不确定的 |
函数f(x)=log2
是( )
| 1+x |
| 1-x |
| A、偶函数 |
| B、奇函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |
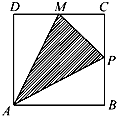 如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )
如图甲所示,点P在边长为1的正方形的边上运动,设M是CD边的中点,则当点P沿着A-B-C-M运动时,以点P经过的路程x为自变量,三角形APM的面积函数的图象形状大致是图乙中的( )