题目内容
集合A={x|x2+3x-10＜0}，B={x|0＜x+1＜4}，则A∩（∁RB）=（ ）
| A、{x|-1＜x＜2} |
| B、{x|-5≤x≤-1或2＜x≤3} |
| C、{x|-5＜x≤-1} |
| D、{x|-5≤x≤-1} |
考点：交、并、补集的混合运算
专题：集合
分析：求出A与B中不等式的解集确定出A与B，求出A与B补集的交集即可．
解答：
解：由A中不等式变形得：（x-2）（x+5）＜0，
解得：-5＜x＜2，即A={x|-5＜x＜2}，
由B中不等式解得：-1＜x＜3，即B={x|-1＜x＜3}，
∴∁RB={x|x≤-1或x≥3}，
则A∩（∁RB）={x|-5＜x≤-1}，
故选：C．
解得：-5＜x＜2，即A={x|-5＜x＜2}，
由B中不等式解得：-1＜x＜3，即B={x|-1＜x＜3}，
∴∁RB={x|x≤-1或x≥3}，
则A∩（∁RB）={x|-5＜x≤-1}，
故选：C．
点评：此题考查了交、并、补集的混合运算，熟练掌握各自的定义是解本题的关键．
练习册系列答案
相关题目
下列命题中的假命题是（ ）
| A、存在x∈R，lg x=0 |
| B、存在x∈R，tan x=1 |
| C、任意x∈R，x3+1＞0 |
| D、任意x∈R，2x＞0 |
幂函数的图象过点（2，8），则它的单调递增区间是（ ）
| A、（0，+∞） |
| B、[0，+∞） |
| C、（-∞，0） |
| D、（-∞，+∞） |
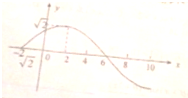已知函数f（x）=Asin（ωt+φ）（A＞0，ω＞0，|φ|＜
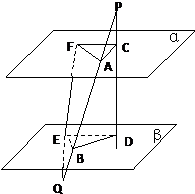如图，线段PQ分别交两个平行平面α、β于A、B两点，线段PD分别交α、β于C、D两点，线段QF分别交α、β于F、E两点，若PA=9，AB=12，BQ=12，△ACF的面积为72，求△BDE的面积．