题目内容
如图展示了一个由区间(0,1)到实数集R的映射过程;区间(0,1)中的实数m对应数轴上的点M,如图①;将线段AB围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为(0,1),如图③.图③中直线AM与x轴交于点N(n,0),则m的象就是n,记作f(m)=n.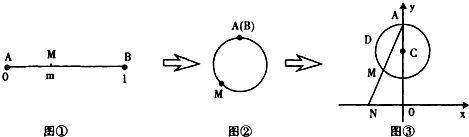
(1)方程f(x)=0的解是 ;
(2)下列说法中正确命题的序号是 .(填出所有正确命题的序号)
①f(
)=1;②f(x)是奇函数;③f(x)在定义域上单调递增;④f(x)的图象关于点(
,0)对称;⑤f(x)>
的解集是(
,1).

(1)方程f(x)=0的解是
(2)下列说法中正确命题的序号是
①f(
| 1 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
考点:命题的真假判断与应用
专题:新定义,函数的性质及应用,不等式的解法及应用
分析:借助于图形观察,方程f(x)=0,即N(0,0),M在A的正下方,即可得到m;
先利用f(
)=-1,判断出①错;在有实数m所在区间(0,1)不关于原点对称,知②错;
从图形上可得f(x)在定义域上单调递增,③对;先找到f(
)=0,再利用图形判断④对;
当f(x)=
时,即N(
,0),直线AN:x+
y=
,代入圆方程求得M的坐标,即可得到m,再由f(x)的单调性,即可判断⑤.
先利用f(
| 1 |
| 4 |
从图形上可得f(x)在定义域上单调递增,③对;先找到f(
| 1 |
| 2 |
当f(x)=
| 3 |
| 3 |
| 3 |
| 3 |
解答:
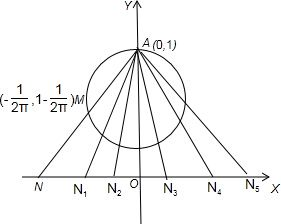 解:如图,因为M在以(0,1-
解:如图,因为M在以(0,1-
)为圆心,
为半径的圆上运动,
方程f(x)=0,即N(0,0),M在A的正下方,
即有AM的弧长为
,即m=
,解得x=
;
对于①,当m=
时.M的坐标为(-
,1-
),
直线AM方程y=x+1,
所以点N的坐标为(-1,0),故f(
)=-1,
即①错;
对于②,因为实数m所在区间(0,1)不关于原点对称,所以f(x)不存在奇偶性.故②错;
对于③,当实数m越来越大时,
如图直线AM与x轴的交点N(n,0)也越来越往右,
即n也越来越大,所以f(x)在定义域上单调递增,即③对;
对于④,当实数m=
时,对应的点在点A的正下方,
此时点N(0,0),所以f(
)=0,
再由图形可知f(x)的图象关于点(
,0)对称,即④对;
对于⑤,当f(x)=
时,即N(
,0),直线AN:x+
y=
,代入圆方程x2+(y-1+
)2=
,
求得M(
,1-
),|AM|=
,AM的弧长为1-
=
,由③可得解集是(
,1).则⑤错误.
故答案为:
,③④.
 解:如图,因为M在以(0,1-
解:如图,因为M在以(0,1-| 1 |
| 2π |
| 1 |
| 2π |
方程f(x)=0,即N(0,0),M在A的正下方,
即有AM的弧长为
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
对于①,当m=
| 1 |
| 4 |
| 1 |
| 2π |
| 1 |
| 2π |
直线AM方程y=x+1,
所以点N的坐标为(-1,0),故f(
| 1 |
| 4 |
即①错;
对于②,因为实数m所在区间(0,1)不关于原点对称,所以f(x)不存在奇偶性.故②错;
对于③,当实数m越来越大时,
如图直线AM与x轴的交点N(n,0)也越来越往右,
即n也越来越大,所以f(x)在定义域上单调递增,即③对;
对于④,当实数m=
| 1 |
| 2 |
此时点N(0,0),所以f(
| 1 |
| 2 |
再由图形可知f(x)的图象关于点(
| 1 |
| 2 |
对于⑤,当f(x)=
| 3 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2π |
| 1 |
| 4π2 |
求得M(
| ||
| 4π |
| 1 |
| 4π |
| 1 |
| 2π |
| 1 |
| 6 |
| 5 |
| 6 |
| 5 |
| 6 |
故答案为:
| 1 |
| 2 |
点评:本题考查了在新定义的条件下解决函数问题,是一道很好的题.关于新定义型的题,关键是理解定义,并会用定义来解题.

练习册系列答案
相关题目
已知函数f(x)是定义在R上的偶函数,且对任意的实数x1≠x2(x1>0,x2>0)时,有
>0成立,如果实数t满足f(lnt)-f(1)≤f(1)-f(ln
),那么t的取值范围是( )
| f(x1)-f(x2) |
| x1-x2 |
| 1 |
| t |
| A、(0,e] | ||
B、[0,
| ||
| C、[1,e] | ||
D、[
|
如图所示是一个几何体的三视图,则该几何体的表面积为( )


A、4+2
| ||
B、2+
| ||
C、2+2
| ||
D、4+
|
 已知点G是△ABC的外心,
已知点G是△ABC的外心,| GA |
| GB |
| GC |
| GA |
| AB |
| AC |
| 0 |
| OA |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
直线y=k(x-m)(k,m∈R且k≠0)与圆x2+y2=1交于A,B两点,记以Ox为始边(O为坐标原点),OA,OB为终边的角分别为α,β,则|sin(α+β)|的值( )
| A、只与m有关 |
| B、只与k有关 |
| C、与m,k都有关 |
| D、与m,k都无有关 |