题目内容
若tanx＞tan
且x在第三象限，则x的取值范围是 ．
| π |
| 5 |
考点：正切函数的图象
专题：三角函数的图像与性质
分析：根据正切函数的单调性进行求解即可．
解答：
解：∵x在第三象限，
∴tanx＞tan
等价为tanx＞tan（π+
），
即tanx＞tan
，
∵x在第三象限，
∴
+kπ＜x＜kπ+
，k∈Z，
故答案为：
+kπ＜x＜kπ+
，k∈Z
∴tanx＞tan
| π |
| 5 |
| π |
| 5 |
即tanx＞tan
| 6π |
| 5 |
∵x在第三象限，
∴
| 6π |
| 5 |
| 3π |
| 2 |
故答案为：
| 6π |
| 5 |
| 3π |
| 2 |
点评：本题主要考查正切函数的单调性的应用，根据三角函数的图象和性质是解决本题的关键．
练习册系列答案
黄冈小状元解决问题天天练系列答案
相关题目
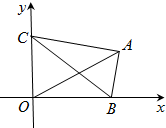已知点G是△ABC的外心，| GA |
| GB |
| GC |
| GA |
| AB |
| AC |
| 0 |
| OA |
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
直线y=k（x-m）（k，m∈R且k≠0）与圆x2+y2=1交于A，B两点，记以Ox为始边（O为坐标原点），OA，OB为终边的角分别为α，β，则|sin（α+β）|的值（ ）
| A、只与m有关 |
| B、只与k有关 |
| C、与m，k都有关 |
| D、与m，k都无有关 |
已知直线ax+by-
=0（a＞l，b＞1）被圆x2+y2-2x-2y-2=0截得的弦长为2
，则ab的最小值为（ ）
| 2 |
| 3 |
A、
| ||
B、
| ||
C、3-2
| ||
D、3+2
|
下列所给的函数中，定义域为[0，+∞）的是（ ）
A、y=
| ||
B、y=x
| ||
| C、y=3-x | ||
| D、y=lgx |
设
、
是平面内所有向量的一组基底，则下面四组向量中，不能作为基底的是（ ）
| e1 |
| e2 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、2
|