题目内容
在数列{an}中,已知a1=3,当n≥2时,
-
=
,求an.
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| 5 |
考点:数列递推式
专题:等差数列与等比数列
分析:由题意可知,数列{
}是以
为首项,以
为公差的等差数列,求出等差数列的通项公式,则an可求.
| 1 |
| an |
| 1 |
| 3 |
| 1 |
| 5 |
解答:
解:由当n≥2时,
-
=
,且a1=3,
可知数列{
}是以
为首项,以
为公差的等差数列,
则
=
+
(n-1)=
n+
=
.
∴an=
.
| 1 |
| an |
| 1 |
| an-1 |
| 1 |
| 5 |
可知数列{
| 1 |
| an |
| 1 |
| 3 |
| 1 |
| 5 |
则
| 1 |
| an |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| 2 |
| 15 |
| 3n+2 |
| 15 |
∴an=
| 15 |
| 3n+2 |
点评:本题考查了数列递推式,考查了等差数列的通项公式,是基础题.

练习册系列答案
相关题目
已知集合M={-1,1},N={x|
<2x<4,x∈Z},则M∩N=( )
| 1 |
| 2 |
| A、{-1,1} | B、{1} |
| C、{0} | D、{-1,0} |
已知函数f(x)定义域为R,f′(x)存在,且f(-x)=f(x),则f′(0)=( )
| A、2 | B、1 | C、0 | D、-1 |
 某同学在研究函数f(x)=
某同学在研究函数f(x)=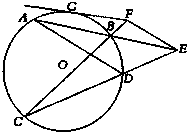 已知:如图,圆O两弦AB与CD交于E,EF∥AD,EF与CB延长线交于F,FG切圆O于G.
已知:如图,圆O两弦AB与CD交于E,EF∥AD,EF与CB延长线交于F,FG切圆O于G.